Общие знаменатели: 294 (Дроби 63/294 и 70/294), 42 (дроби 9/42 10/42), 84 (18/84 20/84)
Пошаговое объяснение:
3/14 5/21
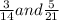
Когда приводим к общему знаменателю, мы умножаем числитель так же, на такое-же число.
Наименьший общий знаменатель, это 42, находится он простым методом подбора. 42 это то число, которое делится на 14 и на 21.
Решать не надо, но расскажу принцип как получается дробь.
Мы нашли общий знаменатель это 42, 42 делится на 14 и на 21.
Разделим 42 на 14, это 3. Разделим 42 на 21 это 2.
Значит, 3/14 надо домножить знаменатель и числитель на 3, а в дроби 5/21 надо домножать на 2.
Значит мы получаем, 3*3/14*3 и 5*2/21*2
Получаем, 9/42 и 10/42.
Дальше, вариант найти общий знаменатель в лоб. Мы просто перемножаем знаменатели и умножаем так же числитель.
Это значит, что общий знаменатель у 14 и 21 будет 14*21 ведь, и так и так делится, и сразу понятно что на что.
Тогда, 3*21/14*21 и 5*14/21*14
Получаем, 63/294 и 70/294
Да, может большие числа, но если никак не придумать НОК (в нашем случае это 42) то это действенный вариант, а потом сокращать.
И что бы привести 3 пример знаменателя общего, мы возьмем НОК и просто домножим его на 2, как и числитель в дроби.
Получаем, 9*2/42*2 и 10*2/42*2
18/84 и 20/84
Пошаговое объяснение:
1) Эта запись означает, что если x стремится к x0=3 справа, то есть оставаясь больше, чем 3, то значения функции f(x) при этом неограниченно приближаются к числу 7. Иными словами: сколь бы малое число ε>0 ни взять, найдётся такое положительное число δ, что для всех значений x из интервала (3; 3+δ) будет выполняться неравенство /f(x)-7/<ε (здесь чертами / / обозначен модуль).
2) Буквами sup обозначается точная верхняя граница некоторого множества. В данном случае таким множеством является множество значений функции f(x) из интервала x∈[1;2]. Это значит, что либо наибольшее значение функции f(x) на этом интервале равно 5, либо значения этой функции в одной или нескольких точках данного интервала неограниченного приближаются к числу 5, то есть предел функции f(x) в этой точке (в этих точках) равен 5. Обобщая, можно сказать так: запись sup f(x)=5 при x∈[1;2] означает, что предел функции f(x) в одной, нескольких или даже во всех точках интервала x∈[1;2] равен 5.
Далее решаем 2 ур-ия
и
ответ: 0;