Пошаговое объяснение:
1.
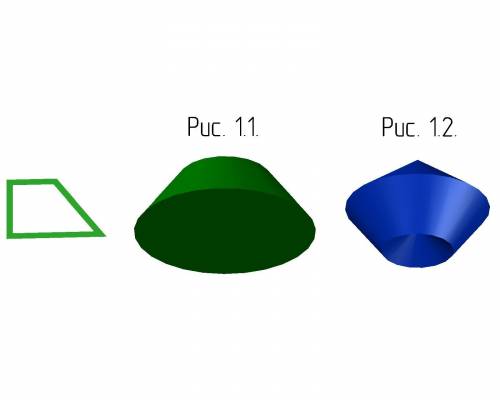
1.1. При вращении вокруг прямой боковой стороны получим усеченный конус. См. рис. 1.1.
1.2. При вращении вокруг наклонной боковой стороны, получим сложную фигуру в виде "летающей тарелки" в виде двух склеенных конусов с общим основанием с конусовидным осевым вырезом с одной из сторон. См. рис. 1.2.
2.
2.1. Для получения прямого конуса нужно вращать прямоугольный треугольник вокруг его катета.
2.2. Для получения прямого конуса нужно вращать равнобедренный треугольник вокруг его высоты к основанию.
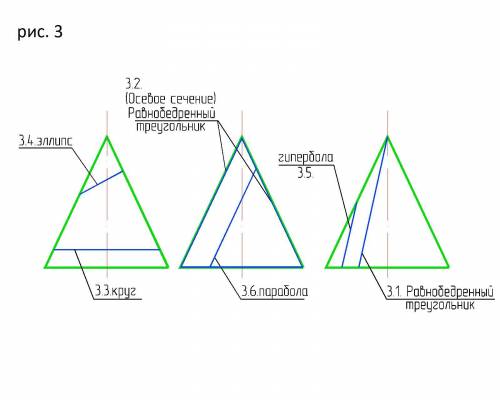
3. Конус и плоскость могут иметь в пересечении часть конуса. В этом случае мы получаем различные сечения. См. рис. 3.
3.1. Пусть плоскость сечения проходит через две образующие конуса. Через две прямые, на которых лежат какие-нибудь две образующие конуса, можно провести единственную плоскость α. Эта плоскость пересечет основание конуса по хорде, а боковую поверхность — по двум образующим. Общей частью этой плоскости и конуса является равнобедренный треугольник.
3.2. Если плоскость α проходит через ось конуса, то полученный в сечении треугольник называется осевым сечением конуса.
3.3. Конус можно пересечь плоскостью α, перпендикулярной к его оси. В этом случае плоскость сечения параллельна плоскости основания, а сечением конуса является круг.
3.4. Если боковую поверхность конуса пересечь плоскостью β так, чтобы эта плоскость не пересекала его оснований и не была перпендикулярной к оси конуса, то в сечении получается эллипс.
3.5. Если плоскость α не проходит через ось и вершину конуса, но пересекает его основание под таким наклоном, что сечение не пересекает ось конуса, то сечением будет гипербола, ограниченная плоскостью основания.
3.6. Если плоскость α не проходит через ось и вершину конуса, но пересекает его основание под таким наклоном, что сечение пересекает ось конуса, то сечением будет парабола, ограниченная плоскостью основания.
4. Для фигуры вращения.
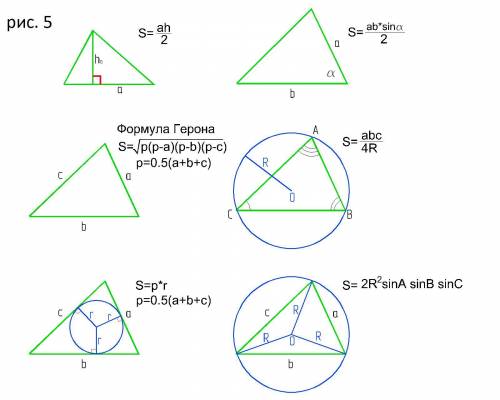
5. См. рис. 5
6.
sin30°=0.5
sin60°=√3/2
sin90°=1
cos30°=√3/2
cos60°=0.5
cos90°=1
7. Т.к. вращение равнобедренного треугольника вокруг его основания образует два равных прямых конуса, соединенных по основанию, то площадь поверхности такой фигуры равна двум площадям боковой поверхности конуса с образующей 7 и радиусом основания 7*sin45°.
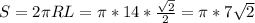 ед.²
ед.²