Куб натурального числа n можно представить в виде n слагаемых, образующих арифметическую прогрессию с разностью 2.
Доказательство:
Если n — число нечётное:
Пусть средний член равен n². Тогда сумма членов этой прогрессии равна n² + n² - 2 + n² + 2 + ... = n² + n² + n² + ... (n раз) = n² * n = n³.
Если n — число чётное:
Пусть средние члены (по счёту n/2 и n/2 + 1) равны n²-1 и n²+1. Сумма членов прогрессии равна: n² - 1 + n² + 1 + n² - 3 + n² + 3 + ... = n² + n² + n² + ... (n раз) = n² * n = n³.
Во всех возможных случаях мы смогли представить куб натурального числа в виде n слагаемых, что и требовалось доказать.
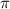в математике, по определению, равно отношению длинны 
произвольной окружности к диаметру 
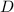той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
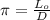формула [1] ;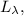
составляющую 
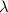часть от длины всей окружности, в данном конкретном случае 
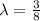от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть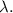 
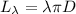формула [2] ;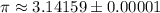
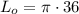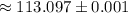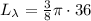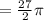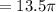см 
см ;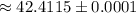
см 
см 
см 
см ;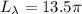
см ;
см .
Р=2*(6+3)=18 см