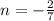 - знаменатель обращается в 0.
- знаменатель обращается в 0.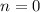 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)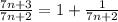

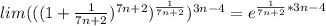 (при
(при  →∞)
→∞)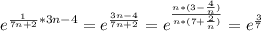 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→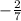
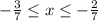 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
42 = 2 · 3 · 7
60 = 2 · 2 · 3 · 5
Общие множители чисел: 2; 3
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (42; 60) = 2 · 3 = 6
28 = 2 · 2 · 7
33 = 3 · 11
Общие множители чисел: 1
НОД (28; 33) = 1
26 = 2 · 13
65 = 5 · 13
130 = 2 · 5 · 13
Общие множители чисел: 13
НОД (26; 65; 130) = 13
72 = 2 · 2 · 2 · 3 · 3
432 = 2 · 2 · 2 · 2 · 3 · 3 · 3
792 = 2 · 2 · 2 · 3 · 3 · 11
Общие множители чисел: 2; 2; 2; 3; 3
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (72; 432; 792) = 2 · 2 · 2 · 3
45 = 3 · 3 · 5
81 = 3 · 3 · 3 · 3
Общие множители чисел: 3; 3
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (45; 81) = 3 · 3 = 9
75 = 3 · 5 · 5
90 = 2 · 3 · 3 · 5
Общие множители чисел: 3; 5
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (75; 90) = 3 · 5 = 15
48 = 2 · 2 · 2 · 2 · 3
240 = 2 · 2 · 2 · 2 · 3 · 5
264 = 2 · 2 · 2 · 3 · 11
Общие множители чисел: 2; 2; 2; 3
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (48; 240; 264) = 2 · 2 · 2 · 3 = 24
163 = 163
310 = 2 · 5 · 31
997 = 997
Общие множители чисел: 1
НОД (163; 310; 997) = 1