24 - сумма чисел в вершинах
Пошаговое объяснение:
Обозначим числа в вершинах квадрата как a, b, c, d.
Тогда, возле каждой стороны квадрата стоят произведения ab, bc, cd, ad, сумма которых равна 143.
Составим уравнение:
ab+bc+cd+ad=143
(ab+bc)+(cd+ad)=143
b(a+c)+d(a+c)=143
(a+c)(b+d)=143
Число 143 имеет 4 делителя, на которые оно делится без остатка и дробей: 1, 143, 11, 13. Числа 1 и 143 в расчёт не принимаем, т.к. по условию, в вершинах квадрата написали 4 натуральных числа.
Остаются два числа - 11 и 13:
143 = 11*13 = 13*11
Следовательно, a+c=11 и b+d=13 или a+c=13 и b+d=11
Но в любом случае, (a+c)+(b+d) = а + b + с + d = 11 + 13 = 24
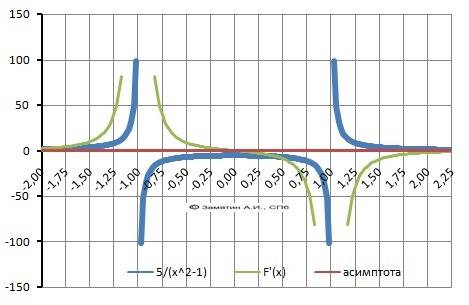
ответ: Рисунок с графиком функции в приложении.
ДАНО: Y(x) = 5/(x²-1).
Пошаговое объяснение:
1. Область определения. (x²-1) = (x-1)*(x+1) ≠ 0. x ≠ +/- 1 - разрывы.
D(y) = (-∞;-1)∪(-1;1)∪(1;+∞)
2. Вертикальные асимптоты: Y = -1, Y = 1.
3. Пересечение с осью Х - Y(x) = 0 - нет.
4. Пересечение с осью Y - Y(0) = -5.
5. Поведение в точках разрыва.
lim(-1-) = +∞, lim(-1+) = -∞, lim(1-) = -∞, lim(1-) = +∞,
Горизонтальная асимптота: Y = 0.
6. Интервалы знакопостоянства.
Положительна: X∈(-∞;-1)∪(1;+∞), отрицательна: X∈(-1;1)
7. Проверка на чётность.
Y(-x) = Y(x) - функция чётная.
8. Поиск экстремумов - корни первой производной.
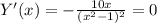- корень Х = 0.
9. Локальный экстремум. Максимум Y(0) = -5.
10. Интервалы монотонности.
Возрастает: X∈(-∞;-1)∪(-1;0), убывает: X∈(0;1)∪(1;+∞)
11. Поиск перегибов - корни второй производной.
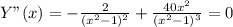- корней нет.
12. Выпуклая - "горка" - X∈(-1;1); вогнутая - "ложка" - X∈(-∞;-1)∪(1;+∞).
13. График на рисунке в приложении.
