Вероятность вытащить из второй урны белый шар
p = 100/ (100+100) = 1/2
В эксперименте из второй урны вытащили 1/2 белого шара и переложили в первую . Там стало 3/2 белого шара из 4 .
Вероятность вытащить оттуда белый шар в результате эксперимента
P ( Б ) = (3/2) / 4 = 3/8
По формуле Байеса вероятность того что вынутый шар находился ранее во второй урне при условии что вытащен белый шар равна
P ( 2 | Б ) = P ( Б | 2 ) * P ( 2 ) / P ( Б )
Р ( Б | 2 ) - Вероятность белого шара приусловии что он из второй урны = p=1/2
P( 2 ) - Вероятность что вытащенный шар из второй урны - в первой урне всегда один шар из четырех из второй урны = 1/4
Итого
P ( 2 | Б ) = (1/2) * (1/4) / (3/8) = 1/3
Чтобы из числа можно было сделать все шесть различных двухзначных чисел, необходимо, чтобы исходное число было трехзначным и все цифры в нем были разные, представим это число в виде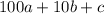 
.
А сумма всех шести различных двухзначных чисел будет такая:
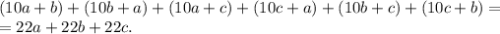
При этом (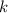
натуральное):
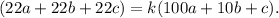
Представим теперь, что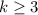 
, то есть:
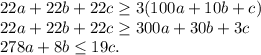
Но это противоречие, так как правая часть по-любому больше левой, а здесь она меньше. Поэтому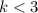 
.
Итак, нужно рассмотреть два случая:
1). 
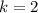. Тогда:
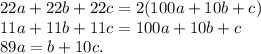
Нетрудно понять, что в натуральных однозначных числах здесь всего одно решение: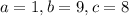 
.
А нужное число - это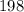 
.
2). Случай посложнее: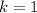 
.
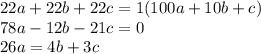
Если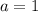 
уравнение принимает вид 
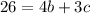, и, тогда в вышеуказанных условиях у него такое одно решение: 
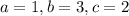. Число - 
.
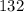Ну а теперь пусть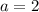 
и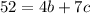 
. Здесь методом подбора: 
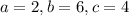. А число - 
.
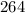И последний случай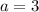 
, то есть 
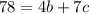, где, подбором, 
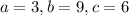. Число 
.
Делаем вывод, что Вася богатый и у него в доме четыре (по крайней мере!) квартиры.
