1) 15 см и 18 см
2) 75√3 см²
Пошаговое объяснение:
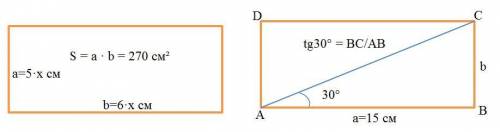
1) Площадь прямоугольника вычисляется по формуле S = a • b, где a и b стороны прямоугольника.
Пусть х>0 коэффициент пропорциональности. Тогда одна сторона прямоугольника равна a=5•х см, а вторая b=6•х см (см. рисунок). Подставляем в формулу площади и найдём х:
5•х см•6•х см =270 см²
30•х² см²= 270 см²
х²=270:30
x²=9
x=3
Значит, одна сторона a=5•3 см=15 см, другая сторона b=6•3 см = 18 см.
2) Площадь прямоугольника вычисляется по формуле S = a • b, где a и b стороны прямоугольника. По условию a=AB= 15 см, определим b=BC. Диагональ AC делить прямоугольник ABCD на прямоугольные треугольники ABC и ADC (см. рисунок). В треугольнике ABC по определению
tg30° = BC/AB = b/a или b = a• tg30° = 15 см • √3/3=5√3 см.
Тогда S = 15 см • 5√3 см = 75√3 см².
Нельзя.
Пошаговое объяснение:
Число (название города) делится на 3, если сумма его цифр делится на 3. Из города №9 можно попасть в город №6 (69/3=23, 96/3=32), в город №3 (39/3=13, 93/3=31). Больше никакие цифры в сумме с 3, 6, 9 не дают число кратное трем.
→9→6→3→9→6→3→
Из города №1 можно попасть в город №5 (15/3=5, 51/3=17), потом в город №4 (45/3=15, 54/3=18), далее в город №2 (24/3=8, 42/3=14), дальше в город №7 (27/3=9, 72/3=24), потом в город №8 (78/3=26, 87/3=29) и возврат в город №1 (81/3=27,18/3=6).
1→5→4→2→7→8→1