Нули производной: х = 1 и х = -2 (не входит в заданный промежуток).
Находим значения функции на границах заданного промежутка и в экстремальной точке.
у(0) = -16, у(1) = -27, у(3) = 125.
Значит, минимум в точке х = 1, максимум в точке х = 3.
3) 1. Разложим знаменатель на множители: y=2x/((x-4)(x+4)).
Область определения функции - вся числовая ось: D(f) = R кроме х = 4 и х = -4.
2. Функция f (x) = 2x/(x2 - 16) непрерывна на всей области определения.
Точки, в которой функция точно не определена (разрыв функции): х = 4 и х = -4.
Область значений функции приведена в пункте 8.
3. Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в 2x/(x2 - 16).
у = 2*0/(02 - 16) = 0.
Результат: y = 0. Точка: (0; 0).
4. Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
2x/(x2 - 16)= 0
Решаем это уравнение и его корни будут точками пересечения с X:
2х = 0,
х = 0.
Результат: y=0. Точка: (0; 0).
5. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = (2*(х2 - 16))-2х*2х)/(х2 - 16)2,
y' = -(2(х2 + 16))/(х2 - 16)2 = 0
Решаем это уравнение и его корни будут экстремумами (достаточно нулю приравнять множитель числителя в скобках): х2 + 16 = 0, х2 = -16.
Результат: нет решения.
Функция не имеет экстремумов.
6. Интервалы возрастания и убывания функции:
С учётом двух точек разрыва функции имеем 3 интервала монотонности функции: (-∞; -4, (-4; 4), (4; ∞).
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -5 -4 0 4 5
y' = -1,01235 - -0,125 - -1,01235
Экстремумов нет.
На всех промежутках функция убывает.
7. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y''=(4x(х2 + 48))/(х2 - 16)3 = 0
Для решения достаточно приравнять нулю числитель уравнения:
4x(х2 + 48) = 0. Множитель в скобках не может быть равен нулю, только х = 0.
Эти и есть точка перегиба графика функции.
Интервалы выпуклости, вогнутости.
Находим знаки второй производной на полученных промежутках.
x = -5 -4 -1 0 1 4 5
y'' = -2,00274 - 0,058074 0 -0,05807 - 2,002743
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый:
Выпуклая на промежутках: (-∞;-4) U (0; 4).
Вогнутая на промежутках: (-4; 0) U (4; +∞).
8. Асимптоты.
Асимтоты бывают трех видов: вертикальные, горизонтальные и наклонные.
а) Вертикальные асимптоты – определены: х = -4 и х = 4.
б) Горизонтальная асимптота у графика функции определяется при нахождении предела функции на бесконечности:
Горизонтальная асимптота – это прямая у = 0 (ось Ох) как предел функции.
С учётом того, что у точек разрыва функции её значение стремится к бесконечности, а при аргументе, стремящемся к бесконечности, функция стремится к нулю, определяем область значений функции: у Є (-∞; ∞).
в) наклонных асимптот нет. Функция f(x) имеет наклонную асимптоту y = k x + b тогда и только тогда, когда существуют конечные пределы k и в в уравнении у = kх + в.
〖 k=lim〗┬( x→±∞)〖(f(x))/x.〗
〖b=lim 〗┬( x→±∞)〖[f(x)-kx].〗
Для данной функции первый из этих пределов равен нулю, поэтому наклонная линия не определяется (она совпадает с горизонтальной асимптотой).
8. Четность и нечетность функции:
Проверим функцию - четна или нечетна с соотношений
Добрый человек добрый кот добрый щенок добрый библиотекарь добрая учителница добрый продавец добрый риэлтор добрый водитель добрый доктор добрый воспитатель 1)Делай другим добро — будешь сам без беды. 2)Делая зло, на добро не надейся. 3)Добра желаешь, добро и делай. 4)Добра ищи, а худо само придет. 5)Добра на худо не меняют. 6)Добрая слава злому ненавистна. 7)Добро быть в радости и жить в сладости. 8)Добро вспомянется, а лихо не забудется. 9)Добро делаем — добро и снится, а худо делаем — худо и снится. 10)Добро не умрет, а зло пропадет.
Встречи со старцами происходят и в наше время. Имеется рассказ, как один из "исследователей" поднялся осенью на одну из вершин Жигулевских гор". Все звуки замерли. И вдруг, где-то совсем рядом, раздался скрип. Кто-то как будто немного приоткрыл свою дверь. Я оглянулся и ничего вокруг не увидел. Да и какую дверь я мог на вершине увидеть. Но скрип раздался снова... Оглянувшись, увидел милого старичка, державшего в руках связку писем. Неподалеку от него, в отвесной скале, виднелась дубовая дверь на ржавых петлях...
– Возьми эти письма себе, – сказал повелительно старичок. – Их написал мне когда-то мой гимназический друг, ставший потом отшельником... И, видя мою окаменелость, он вложил в мои руки довольно тяжелую связку. – Можешь использовать эти письма, как будет угодно, – пояснил старичок и вошел в скалу. Я снова услышал скрип закрываемой двери, и все смолкло... Интересно отметить, что когда, желая снова увидеть старичка, я поднялся на эту гору, никакой скрипучей двери там не нашел. На ее месте, которое я отчетливо запомнил, скала шла гладким сплошняком. Но письма жигулевского отшельника, числом более сотни, перевязанные крест-накрест старой тесемкой, хранятся и поныне у меня. Я часто их читаю...
Вот другой рассказ о "современных подземных старцах". "Группа спелеологов пришла как-то на гору Верблюд. Вечером пошли собирать сучья для костра. Все вернулись, а одного нет. Кто-то видел – прибегал за лопатой, мол, щель нашел, кажется вход в пещеру. Над ним посмеялись – место-то тут хоженное-перехоженное, откуда ей тут быть. А парень как сквозь землю провалился. Пошли на поиски с фонарями. Стали кричать – вроде отозвался кто-то. Двинулись на голос. Пропавший стоит на тропе, видят он вроде не в себе. Когда отошёл немного, рассказал: "Заметил щель в скальной стене, спустился вниз и попал в темный подземный зал. Вдруг под сводами пещеры сияние. В этом сиянии возник старец и говорит: "Рано тебе сюда". И исчез. Перепуганный исследователь и не помнит, как оказался на поверхности". Спелеологи решили, что все это ему привиделось. Встречи со старцами происходят и в наше время. Имеется рассказ, как один из "исследователей" поднялся осенью на одну из вершин Жигулевских гор". Все звуки замерли. И вдруг, где-то совсем рядом, раздался скрип. Кто-то как будто немного приоткрыл свою дверь. Я оглянулся и ничего вокруг не увидел. Да и какую дверь я мог на вершине увидеть. Но скрип раздался снова... Оглянувшись, увидел милого старичка, державшего в руках связку писем. Неподалеку от него, в отвесной скале, виднелась дубовая дверь на ржавых петлях...
– Возьми эти письма себе, – сказал повелительно старичок. – Их написал мне когда-то мой гимназический друг, ставший потом отшельником... И, видя мою окаменелость, он вложил в мои руки довольно тяжелую связку. – Можешь использовать эти письма, как будет угодно, – пояснил старичок и вошел в скалу. Я снова услышал скрип закрываемой двери, и все смолкло... Интересно отметить, что когда, желая снова увидеть старичка, я поднялся на эту гору, никакой скрипучей двери там не нашел. На ее месте, которое я отчетливо запомнил, скала шла гладким сплошняком. Но письма жигулевского отшельника, числом более сотни, перевязанные крест-накрест старой тесемкой, хранятся и поныне у меня. Я часто их читаю...
Вот другой рассказ о "современных подземных старцах". "Группа спелеологов пришла как-то на гору Верблюд. Вечером пошли собирать сучья для костра. Все вернулись, а одного нет. Кто-то видел – прибегал за лопатой, мол, щель нашел, кажется вход в пещеру. Над ним посмеялись – место-то тут хоженное-перехоженное, откуда ей тут быть. А парень как сквозь землю провалился. Пошли на поиски с фонарями. Стали кричать – вроде отозвался кто-то. Двинулись на голос. Пропавший стоит на тропе, видят он вроде не в себе. Когда отошёл немного, рассказал: "Заметил щель в скальной стене, спустился вниз и попал в темный подземный зал. Вдруг под сводами пещеры сияние. В этом сиянии возник старец и говорит: "Рано тебе сюда". И исчез. Перепуганный исследователь и не помнит, как оказался на поверхности". Спелеологи решили, что все это ему привиделось.
1) Дана функция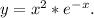
Производная равна
В точке х = 1 производная равна y'(1) = (-1/e)(1 - 2) = 1/e.
Функция в точке х = 1 равна у(1) = 1/е.
ответ: у(кас(1)) =(1/е)(х - 1) + (1/е) = (х/е) - (1/е) + (1/е) = х/е.
2) y' = 4(x - 1)(x + 2)^2.
Нули производной: х = 1 и х = -2 (не входит в заданный промежуток).
Находим значения функции на границах заданного промежутка и в экстремальной точке.
у(0) = -16, у(1) = -27, у(3) = 125.
Значит, минимум в точке х = 1, максимум в точке х = 3.
3) 1. Разложим знаменатель на множители: y=2x/((x-4)(x+4)).
Область определения функции - вся числовая ось: D(f) = R кроме х = 4 и х = -4.
2. Функция f (x) = 2x/(x2 - 16) непрерывна на всей области определения.
Точки, в которой функция точно не определена (разрыв функции): х = 4 и х = -4.
Область значений функции приведена в пункте 8.
3. Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в 2x/(x2 - 16).
у = 2*0/(02 - 16) = 0.
Результат: y = 0. Точка: (0; 0).
4. Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
2x/(x2 - 16)= 0
Решаем это уравнение и его корни будут точками пересечения с X:
2х = 0,
х = 0.
Результат: y=0. Точка: (0; 0).
5. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = (2*(х2 - 16))-2х*2х)/(х2 - 16)2,
y' = -(2(х2 + 16))/(х2 - 16)2 = 0
Решаем это уравнение и его корни будут экстремумами (достаточно нулю приравнять множитель числителя в скобках): х2 + 16 = 0, х2 = -16.
Результат: нет решения.
Функция не имеет экстремумов.
6. Интервалы возрастания и убывания функции:
С учётом двух точек разрыва функции имеем 3 интервала монотонности функции: (-∞; -4, (-4; 4), (4; ∞).
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -5 -4 0 4 5
y' = -1,01235 - -0,125 - -1,01235
Экстремумов нет.
На всех промежутках функция убывает.
7. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y''=(4x(х2 + 48))/(х2 - 16)3 = 0
Для решения достаточно приравнять нулю числитель уравнения:
4x(х2 + 48) = 0. Множитель в скобках не может быть равен нулю, только х = 0.
Эти и есть точка перегиба графика функции.
Интервалы выпуклости, вогнутости.
Находим знаки второй производной на полученных промежутках.
x = -5 -4 -1 0 1 4 5
y'' = -2,00274 - 0,058074 0 -0,05807 - 2,002743
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый:
Выпуклая на промежутках: (-∞;-4) U (0; 4).
Вогнутая на промежутках: (-4; 0) U (4; +∞).
8. Асимптоты.
Асимтоты бывают трех видов: вертикальные, горизонтальные и наклонные.
а) Вертикальные асимптоты – определены: х = -4 и х = 4.
б) Горизонтальная асимптота у графика функции определяется при нахождении предела функции на бесконечности:
lim┬(x→±∞)〖(2x )/(x^2-16)=(2x/x^2 )/(x^2/x^2 -16/x^2 )=0/(1-0)=0.〗
Горизонтальная асимптота – это прямая у = 0 (ось Ох) как предел функции.
С учётом того, что у точек разрыва функции её значение стремится к бесконечности, а при аргументе, стремящемся к бесконечности, функция стремится к нулю, определяем область значений функции: у Є (-∞; ∞).
в) наклонных асимптот нет. Функция f(x) имеет наклонную асимптоту y = k x + b тогда и только тогда, когда существуют конечные пределы k и в в уравнении у = kх + в.
〖 k=lim〗┬( x→±∞)〖(f(x))/x.〗
〖b=lim 〗┬( x→±∞)〖[f(x)-kx].〗
Для данной функции первый из этих пределов равен нулю, поэтому наклонная линия не определяется (она совпадает с горизонтальной асимптотой).
8. Четность и нечетность функции:
Проверим функцию - четна или нечетна с соотношений
f(-x)=f(x) и f(-x)=-f(x). Итак, проверяем:
f(-x)=(-2x)/((-x)^2-16)=-2x/(x^2-16)≠f(x)=-f(x).
3начит, функция является нечётной.
Таблица точек:
x y
-7 -0.424
-6 -0.6
-5 -1.111
-4 -
-3 0.857
-2 0.333
-1 0.133
0 0
1 -0.133
2 -0.333
3 -0.857
4 -
5 1.111
6 0.6
7 0.424