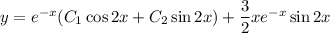1.
1) найти сторону треугольника:
45/3=15
2) найти радиус окружности:
r= /3 *a = / 3 *15 = 5*
3) находим сторону восьмиугольника, используя радиус окружности:
a=2*r*sin180/n в данном случае n=8:
a=2*5 *sin 22.5=10 *sin22.5
2.
вписанный квадрат обозначим abcd, центр окружности - o. o будет находится в точке пересечения диагоналей ac и bd. диагонали квадрата взаимно перепендикулярны и равны a√2, где а - сторона квадрата.
sкв = a²
a² = 72
a = √72
так как диагонали квадрата являются диаметрами для окружности, то радиус окружности будет половиной диагонали:
r = ac/2 = (a√2)/2 = (√72*2)/2 = (√144)/2 = 12/2 = 6
sкруг = πr² = π6² = 36π
ответ: 36π
3.
дано: решение:
r-3см l=2pir*a/360
a=150 l=2pi3*150/360=2,5pi
l-? см
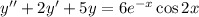
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
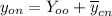
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
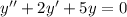
Составим характеристическое уравнение и решим его:
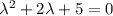
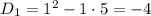
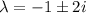
Общее решение однородного уравнения:
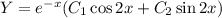
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
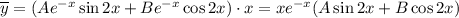
Находим первую производную:
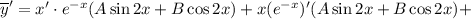
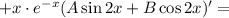
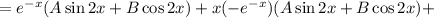
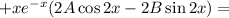
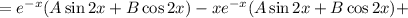
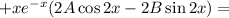
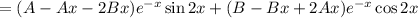
Находим вторую производную:
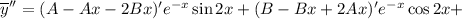
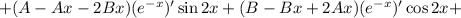
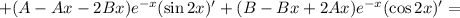
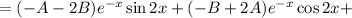

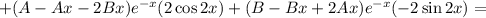
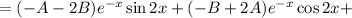
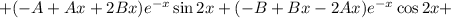
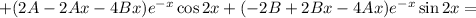
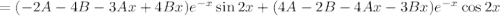
Подставляем в исходное уравнение:
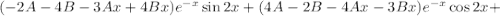
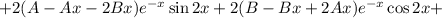
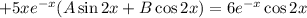
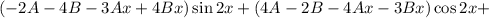
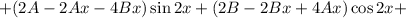
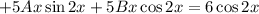
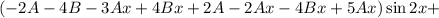
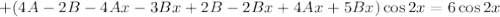
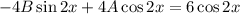
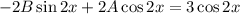
Условие равенства левой и правой частей:
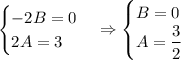
Частное решение данного неоднородного уравнения:
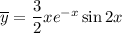
Общее решение данного неоднородного уравнения: