если х=0 то нет смысла
а тут всё правельно
1. (а + b)¹= а + b 2. (а + b)²= а²+ 2аb + b² 3. (а + b)³= а³ +3а²b + 3аb² + b³ Можно раскрыть скобки при вычислении (а +b) и т.д., умножая полученный.Содержание. 1) Понятие бинома Ньютона. 2) Свойства бинома и биномиальных коэффициентов. 3) Примеры решения задач по теме «Бином Ньютона». 4) Выход.Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей §53. Формула бинома Ньютона.БИНОМ НЬЮТОНА. Определение. Двучлен вида a+b называют биномом.Автор : Ван – Хо – Син Виктория Петровна, 7А класс. МОУ СОШ7 г.Амурска. Бином Ньютона.11 класс МКОУ «Усть-Мосихинская СОШ» Новосёлова Е.А.N!n! Волошина Н.Н., Произведение биномов, отличающихся только вторыми членами. Выражение х + а, как и вообще всякий двучлен, называется.Бином Ньютона Бином bis дважды nomen часть Натуральную степень двучлена умели представлять в виде суммы степеней его слагаемых еще в 10 веке индийцы.Бином Ньютона Бином bis дважды nomen часть Натуральную степень двучлена умели представлять в виде суммы степеней его слагаемых еще в 10 веке индийцы.
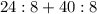
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
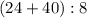
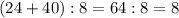В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на , то и их сумма делится на .
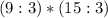
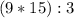
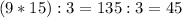
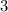,то их произведение делится на 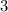" доказанным.
!=- не равняется
1)x!=2, т.к в знаменателе получится 0
4)a!=1 т.к в знаменателе получится0
2)b!=√7 т.к в знаменателе получится 0
3)y!=0 и y=3
5)y!=2 и y!=1
6)c!=0 и с!=1.5
в 3 5 6 объяснение анологичное