-23/2 -18/7 -5/2 -8/7 -13/14 -1/7 1/3 2/5 8/15 7/5 233/30 144/15
Пошаговое объяснение:
сперва разберемся с отрицательными дробями. приведем их к общему знаменателю 14:
-16/14 -35/14 -2/14 -13/14 -36/14 - 161/14
располагаем -161/14 -36/14 -35/14 -16/14 -13/14 -2/14
то же проделаем с положительными дробями. общий знаменатель 30:
10/30 12/30 42/30 16/30 288/30 233/30
располагаем 10/30 12/30 16/30 42/30 233/30 288/30
теперь "слепим" все вместе:
-161/14 -36/14 -35/14 -16/14 -13/14 -2/14 10/30 12/30 16/30 42/30 233/30 288/30
теперь придадим дробям первоначальный вид
-23/2 -18/7 -5/2 -8/7 -13/14 -1/7 1/3 2/5 8/15 7/5 233/30 144/15
Пошаговое объяснение:
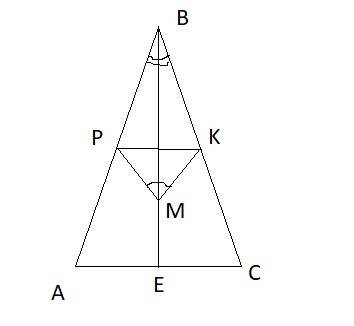
а) Медиана проведенная к основанию равнобедренного треугольника является одновременно его биссектрисой, следовательно ∠PBM = ∠KBM. По условию ∠BMP = ∠BMK.
Следовательно ΔBPM = ΔBKM (у них общая сторона BM. к которой прилегают два равных угла). Из равенства этих треугольников и следует, что ∠BPM= ∠BKM.
б) В пункте а) доказано, что ΔBPM = ΔBKM, откуда следует, что BP = BK. Следовательно PK || AC.
А AC ⊥ BE (т.к. медиана проведенная к основанию равнобедренного треугольника является одновременно его высотой). Значит и PK ⊥ BE ⇒ PK ⊥ BM