Cумма кредита S=220 тыс руб.
Каждый январь начисляются проценты на остаток.
r%= 0,01·r
Обозначим
1+0,01·r= k
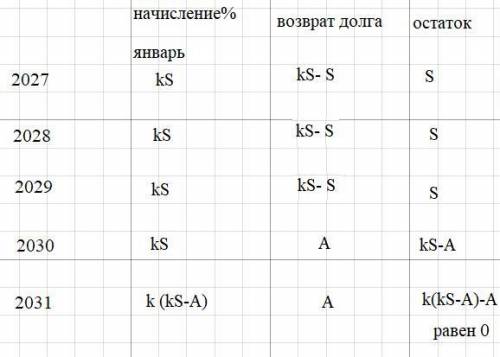
( cм схему начисления и остатки к таблице)
Уравнение 1:
k·(kS–A)–A=0
Уравнение 2:
3·(kS–S)+2A=420
S=220
Решаем систему уравнений:
{k(220k−A)−A=03(220k−220)+2A=420
{220k2=A(k+1)660k−660+2A=420
⎧⎩⎨A=220k2k+1660k+2220k2k+1=1080 {A=220k2k+166k(k+1)+44k2=108(k+1)
{A=220k2k+155k2−21k−54=0 D=212–4·55·(–54)=441+11880=12321=1112
k=1,2 второй корень отрицательный
1+0,01r=k ⇒ 1+0,01r=1,2 ⇒ 0,01·r=0,2 ⇒ r=20%
О т в е т. 20%
___
[k] [б]
[т] [р] [a] [д] [е] [с] [к] [a] [н] [ц] [и] [я]
[к] [л]
[х] [л] [о] [р] [о] [ф] [и] [т] [у] [м] [ь]
[и] [и] [у] [з]
[а] [a] [с] [а] [л] [o] [э]
[н] [л] [м]
[a] [к] [и]
[г] [е] [р] [а] [н] [ь] [н]
1) Обозначим меньшую сторону через Х метров
тогда вторая сторона равна (Х + 8) м.
2) Так как площадь равна 48 м², то можем записать:
Х(Х + 8) = 48
Х² + 8Х - 48 = 0
3) Решаем это квадратное уравнение. Так как коэффициент при Х² равен 1, то корни уравнения находим по теореме Виетта.
Х₁ = 4 , Х₂ = -12 (отрицательное значение не подходит)
4) Значит ширина площадки 4 м, длина (4+8) = 12 м
5) Периметр площадки равен:
Р = 2*(4+12) = 32 м
6) Количество упаковок материала для бордюра:
32/5 = 6,4 ≈ 7 упаковок