Для этого решим уравнение:
х - 1/х = 0;
х²/х - 1/х = 0;
(х² - 1) / х = 0;
(х -1) * (х + 1) / х = 0.
Следовательно, значения х = -1 и х = 1 являются корнями данного уравнения и функция y = x - 1/x пересекается с осью ОХ в точках с абсциссами -1 и 1.
Найдем производную данной функции:
y' = (x - 1/x)' = x + 1/х².
Найдем значения производной в точках х = -1 и х = 1:
y'(-1) = -1 + 1/(-1)² = -1 + 1 = 0;
y'(1) = 1 + 1/(1)² = 1 + 1 = 2.
Запишем уравнение касательной к графику функции y = x - 1/x в точке х = -1:
у = y'(-1)(х - (-1));
у = 0.
Запишем уравнение касательной к графику функции y = x - 1/x в точке х = 1:
у = y'(1)(х - 1);
у = х - 1.
ответ: уравнение касательной в точке х = -1: у = 0; уравнение касательной в точке х = 1: у = х - 1.
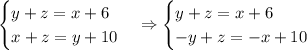

(1,8 - 0,3*у)*(2*у+9) = 0
Раскрываем скобки
3,6*у + 16,2 - 0,6*у² - 2,7*у = 0
Приводим подобные члены
-0,6*у² +0,9*у + 16,2 = 0 - квадратное уравнение.
Находим дискриминант - D= 39,69 и √39,69 =6,3 и
корни х1= - 4,5 х2 = 6 - ОТВЕТ
2)
(5у+4)*(1,1у - 3,3) = 0
Раскрываем скобки.
5,5*у² - 16,5*у + 4,4*у - 13,2 = 0
Приводим подобные члены уравнения.
5,5*у² - 12,1*у - 13,2 = 0
Решаем квадратное уравнение.
Дискриминант - D = 436.81.
Корни - х1=3 х2 = -0,8 - ОТВЕТ.
3)
(3*m+5):4 = (5m+1):3
Приводим к общему знаменателю.
9*m+15 = 20*m+4
11*m = 11
m = 11:11 = 1 - ОТВЕТ
4)
(5*х+3):5 = (х-5):8
40*х + 24 = 5*х - 25
35*х = - 49
х = -49/35 = - 1 2/5 = -1,4 - ОТВЕТ