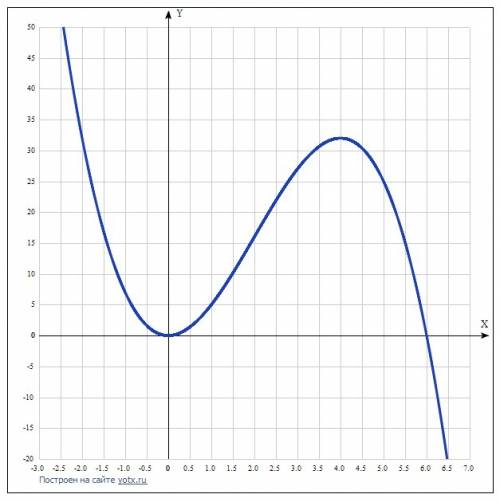
Область определения функции. ОДЗ:-∞<x<∞
Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в =-x³+6x².
Результат: y=0. Точка: (0, 0)
Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
-x³+6x²= 0
Решаем это уравнение и его корни будут точками пересечения с X:
-x3+6x² = -x²(х-6) = 0
x=0. Точка: (0, 0)
x=6. Точка: (6, 0) .
Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=-3x² + 12х=0
Решаем это уравнение и его корни будут экстремумами:
-3x² + 6х = -3x(х-4) = 0.
x=0. Точка: (0, 0)
x=2. Точка: (4, 32)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке: x_{2} = 0.
Максимум функции в точках: x_{2} = 4.
Возрастает на промежутке [0, 4].
Убывает на промежутках (-oo, 0] U [4, oo).
2186 см2
Пошаговое объяснение:
AB=CD — боковые стороны;
AD= 26 см;
BC= 10 см;
O∈AD .
1. Центр окружности, описанной около равнобедренной трапеции, который находится на большем основании, делит его на две равные части:
AO=OD=R=12×AD=12×26=13 см.
2. В равнобедренной трапеции AE и FD можно найти, зная основания:
AE=FD=AD−BC2=26−102=162=8 см.
Вычисляем EO и OF :
EO=OF=R−AE=13−8=5 см.
3. Так как ΔEBO — прямоугольный, то высоту трапеции BE можно найти по теореме Пифагора:
BE=R2−EO2−−−−−−−−√=132−52−−−−−−−√=169−25−−−−−−−√=144−−−√=12 см.
4. Вычисляем площадь трапеции:
S=AD+BC2×BE=26+102×12=18×12=216 см2 .
х - вагонов было
16+х - вагонов стало
6/(16+х)=1/9
16+х=54
х=54-16
х=38 - было первоначально вагонов