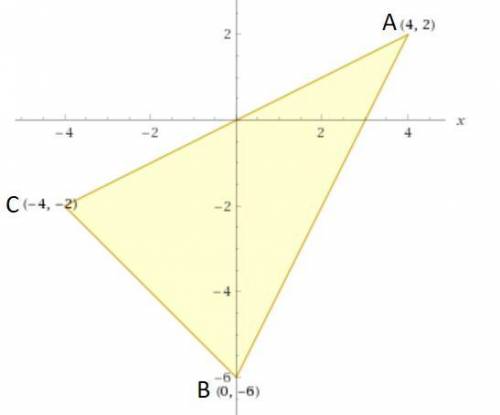
Даны вершины треугольника А (4;2), В (0;-6), С (-4;-2).
1) Уравнение стороны АС этого треугольника в различных формах, координаты направляющего и нормального векторов этой прямой.
Направляющий вектор АС = (-4-4; -2-2) = (-8; -4).
Каноническое уравнение АС: (х - 4)/(-8) = (у - 2)/(-4).
Общее: -4х + 16 = -8у + 16,
-4x + 8y = 0, x - 2y = 0,
С угловым коэффициентом у = (1/2)х.
Если прямую линию на плоскости определяет общее уравнение прямой , то коэффициенты А и B представляют собой соответствующие координаты нормального вектора этой прямой.
Для стороны АС общее уравнение x - 2y = 0, значит, нормальный вектор к стороне АС имеет координаты (1; -2).
б) Уравнения медианы к стороне АВ и высоты к стороне АС.
Точка С2 как середина АВ имеет координаты:
С2 = (4+0)/2; (2-6)/2) = (2; -2). Вектор СС2 = (2+4; -2+2) = (6; 0).
Вектор медианы СС2 имеет координату по у, равную 0, поэтому это горизонтальная линия. Её уравнение у = -2 (у точек С и С2 у = -2).
Для высоты к стороне АС используем свойство: угловой коэффициент к = -1 / к(АС) = -1 / (1/2) = -2.
Тогда уравнение высоты к АС имеет вид у = 2х - 6 с учётом координат точки В.
в) Уравнение прямой параллельной стороне АС, проходящей через вершину В треугольника.
Эта прямая имеет угловой коэффициент такой же, как и сторона АС.
у = (1/2)х + в. Для определения параметра в подставим координаты точки В. -6 = (1/2)*0 + в. Отсюда в = -6. Получаем уравнение у = (1/2)х - 6.
а)10 000-(5200+2400):200=?
Порядок действий:
а) 10000³⁾–(5200¹⁾+2400)²⁾:200 =
1)5200+2400=7600
2)7600:200=38
3)10000-38=9962
а) 10000–(5200+2400):200=9962
б)49000+(6000–3300):300=?
Порядок действий:
б)49000³⁾+(6000¹⁾–3300)²⁾:300=
1)6000-3300=2700
2)2700:300=9
3)49000+9=49009
б)49000+(6000–3300):300=49009
в)4900–8000:(12243–11243)=?
Порядок действий:
в)4900³⁾–8000²⁾:(12243¹⁾–11243)=
1)12243-11243=100
2)8000:1000=8
3)4900-8=4892
в)4900–8000:(12243–11243)=4892
г)30000:(123+177)+400=?
Порядок действий:
г)30000²⁾:(123¹⁾+177)³⁾+400=
1)123+177=300
2)30000:300=100
3)100+400=500
г)30000:(123+177)+400=500
б) ложно
в) ложно
г) истино