(см. объяснение)
Пошаговое объяснение:
 , ОДЗ:
, ОДЗ: 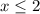 .
.
Заметим, что  является корнем уравнения при любом значении параметра. Тогда нужно, чтобы уравнение
является корнем уравнения при любом значении параметра. Тогда нужно, чтобы уравнение  имело ровно один корень принадлежащий ОДЗ и не равный двум.
имело ровно один корень принадлежащий ОДЗ и не равный двум.
Введем замену 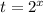 . Откуда
. Откуда 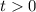 .
.
Тогда уравнение примет вид:

Переформулируем условие задачи:
Найти все значение параметра  , при каждом из которых записанное выше уравнение имеет ровно один корень, принадлежащий промежутку
, при каждом из которых записанное выше уравнение имеет ровно один корень, принадлежащий промежутку  .
.
Введем функцию  . Это парабола, ветви которой направлены вверх, а координата вершины имеет значение
. Это парабола, ветви которой направлены вверх, а координата вершины имеет значение  .
.
Отрисовав возможные расположения парабол, учитывая расположение ее вершины, перейдем к системам:
(я рисовать их не буду, так как на компьютере это неудобно + вы говорите, что уже сами задачу решили)
 /или/
/или/ 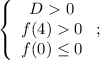
Выполним необходимые вычисления:

Тогда записи примут вид:
 /или/
/или/ 
Итого при ![a\in\left(-1;\;0\right]\cup\left\{\dfrac{3}{2}\right\}\cup\left[3;\;4\right)](/tpl/images/2009/9621/e2fe0.png) исходное уравнение имеет ровно два различных корня.
исходное уравнение имеет ровно два различных корня.
Задание выполнено!
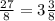 ,
, 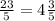 ,
, 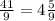 .
.
Пошаговое объяснение:
Перед нами неправильные дроби, то есть такие дроби, в которых в числителе несколько целых значений дроби, плюс остаток от деления числителя на знаменатель.
Запишем первую дробь, 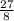 . Данную дробь невозможно сократить ввиду того, что числитель не поделится на 2 без остатка, а знаменатель на 3, на который можно поделить числитель. Другими словами, это несократимая неправильная дробь.
. Данную дробь невозможно сократить ввиду того, что числитель не поделится на 2 без остатка, а знаменатель на 3, на который можно поделить числитель. Другими словами, это несократимая неправильная дробь.
Чтобы привести ее в правильный вид, достаточно посчитать, сколько раз число 27 поделится на 8 без остатка, то есть: 8+8+8=24 и 3 в остатке. То есть, дробь 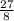 имеет вид:
имеет вид: 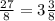 .
.
Вторая и третья дроби рассчитываются по аналогичному алгоритму.
Для второй дроби находим, сколько раз число 23 делится на 5 без остатка: 5+5+5+5=20 и 3 в остатке.
Поэтому, дробь 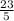 имеет вид:
имеет вид: 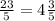 .
.
В третьей дроби получаем: 9+9+9+9=36 и 5 в остатке.
Поэтому, дробь 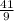 имеет вид:
имеет вид: 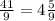 .
.
4 см
ас * кос а =10*0.4=4см.