Это показательное уравнение вида 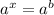 , где
, где 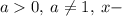 неизвестная переменная.
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения 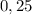 представить в виде числа со степенью так, чтобы в основании было число
представить в виде числа со степенью так, чтобы в основании было число 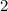 . Это явно число
. Это явно число 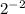 (проверка:
(проверка: 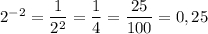 ).
).
Значит теперь, когда наше показательное уравнение имеет вид 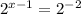 , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение 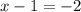 после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е.
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 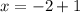 .
.
Из этого следует, что ответ нашего показательного уравнения равен 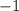 .
.

Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -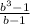 · X
· X
После четвертой выплаты сумма оставшегося долга равна:
S4 = 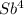 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 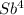 -
- 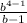 · X
· X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 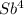 -
- 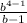 · X = 0.
· X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =  рублей
рублей
б) 4774
в) 12810
г)3125
д)35
е)264