1) Уравнения прямой проходящей из точек (х1; у1) и (х2; у2) такой:
(х-х1)/(х2-х1)=(у-у1)/(у2-у1).
Тогда получаем:
(х-(-1))/(1-(-1))/=(у-1)/(0-1).
(х+1)/2=(у-1)/(-1).
Умножим на (-2):
-(х+1)=2 (у-1).отсюда получим:
у-1=-0,5 (х+1).
у=-0.5х-0.5+1.
у=-0.5х+0.5-искомая прямая.
2)
Вектор CD имеет координаты ( -6; -2) , из координат конца вычли координаты начала. Вектора ВА и СD равны.
Точка А получается сдвигом точки В на вектор ВА равный вектору СD .
Поэтому х(А)=x(В)+x(CD) ⇒ х(А)=0,
у(А)=у(В)+у(CD) ⇒ у(А)=5+(-2)= 3.
Значит А(0 ; 3).
О-середина диагонали АС.
Х(О) =(0+7) :2=3,5
У(О) =(3+2) :2=2,5.
О( 3,5 ;2,5 )
3)

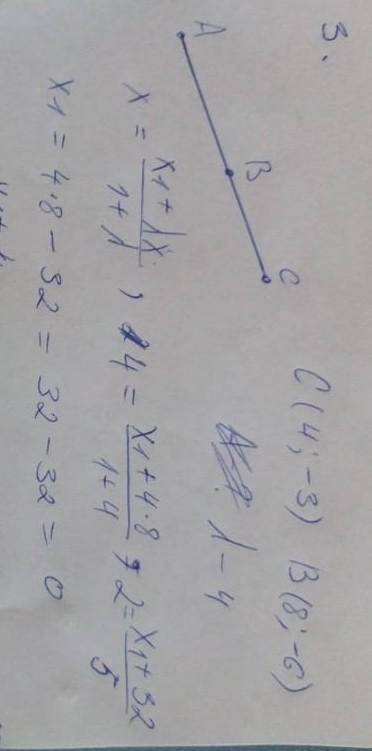
43+6=49
Удачи)