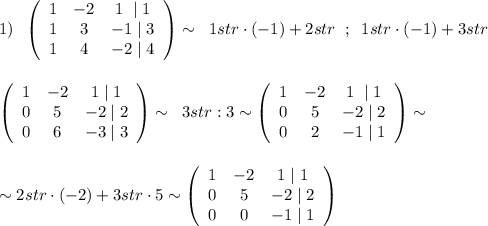
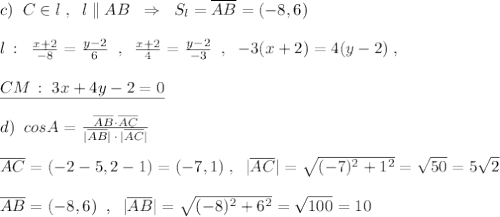
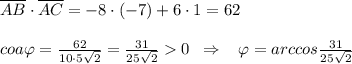
Пошаговое объяснение:
Из условия можно составить 4 уравнения с четырьмя неизвестными:
A + B = 8
A + C = 13
B + D = 8
C - D = 6
Выразим А и подставим в другие уравнения:
A = 8 - B
8 - B + C = 13 C - B = 5
B + D = 8
C - D = 6
Выразим С и подставим в другие:
C = B + 5
B + D = 8
B + 5 - D = 6 B - D = 1
Сложим два последних уравнения:
B + D = 8
B - D = 1
2B = 9 B = 4,5
В нашли, находим D:
B - D = 1 D = B - 1 = 4,5 -1 = 3,5
Ищем С и А:
C = B + 5 = 4,5 + 5 = 9,5
A = 8 - B = 8 - 4,5 = 3,5
А = 3,5
В = 4,5
С = 9,5
D = 3,5
Примеры
Неравенства с модулем
|x^2 - 2x + 2| + |2x + 1| <= 5
Линейные
7x - 6 < x + 12
С квадратом
-3x^2 + 2x + 5 <= 0
Со степенью
2^x + 2^3/2^x < 9
С кубом (неравество третьей степени)
2x^3 + 7x^2 + 7x + 2 < 0
С кубическим корнем
cbrt(5x + 1) - cbrt(5x - 12) >= 1
С натуральным логарифмом
(ln(8x^2 + 24x - 16) + ln(x^4 + 6x^3 + 9x^2))/(x^2 + 3x - 10) >= 0
Иррациональные с квадратным корнем
sqrt(x - 2) + sqrt(x - 5) <= sqrt(x- 3)
Показательные неравенства
8^x + 18^x > 2*27^x
Логарифмические неравенства
log(((7 - x)/(x + 1))^2)/log(x + 8) <= 1 - log((x + 1)/(x - 7))/log(x + 8)
Тригонометрические
tg(x - pi/3) >= -sqrt(3)
Квадратное неравенство
25x^2 - 30x + 9 > 0
С четвёртой степенью
(x - 6)^4*(x - 4)^3*(x + 6)/(x - 7) < 0
С дробью
2x^2 - 15x + 35 - 30/x + 8/x^2 >= 0
Решение с целыми числами
(4x^2 - 3x - 1)/(2x^2 + 3x + 1) > 0
Пошаговое объяснение: