10 городов
Пошаговое объяснение:
1) Обозначим количество городов в 1-ой республике за n, а во 2-ой - за m.
2) По условию каждый город в 1-ой респ соединен с каждым городом 2-ой респ и плюс еще со столичным городом, т. е. всего дорог:
1 город с m городами и со столицей m+1 дорог
n городов с m городами и со столицей n*(m+1) дорог
3) Также и с городами во 2-ой респ, но теперь будем считать только те дороги, которые связывают их со столицей, так как мы уже посчитали дороги, связывающие с городами в 1-ой респ. Их будет m.
4) Значит в стране всего n*(m+1)+m=29 дорог и из этого нам надо найти наименьшее значение суммы n+m+1 (включая столицу):
n*(m+1)+m=29
nm+n+m=29
n+m+1=30-nm, Сюда можно подобрать числа n=4 и m=5, так как их значения не могут быть дробными или отрицательными(n,m∈N, след-но n+m+1>0, а значит и 30-nm>0, откуда nm<30 и чтобы равенство n+m+1=30-nm было верным подходят только n=4 и m=5, так как n,m∈N и nm<30)
Следовательно наименьшее количество городов может равнятся n+m+1=4+5+1=10
ответ: 10 городов
1) 23 и 25.
2) 7 и 24.
Пошаговое объяснение:
1) Пусть первое нечетное число равно 
, тогда следующее за ним нечетное число равно 
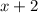. Произведение этих двух чисел равно 575. Составим уравнение.
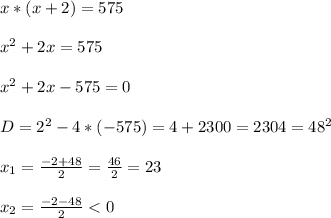
Значит первое число равно 23.
Второе число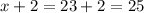 
Проверка: 23·25=575
ответ: 23 и 25.
2) Диагональ делит прямоугольник на два равных прямоугольных треугольника (см. рисунок). В получившемся прямоугольном треугольнике диагональ является гипотенузой, а стороны прямоугольника катетами.
Пусть один катет равен , тогда второй катет равен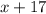 
. Гипотенуза равна 25.
По теореме Пифагора:
Ширина прямоугольника равна 7 см.
Длина прямоугольника равна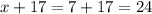 
(см)
ответ: 7 см, 24 см.
