ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
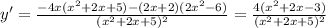
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
1) 84 км.
2) 50 км/час.
Пошаговое объяснение:
От двух лодочных станций расстояние между которыми составляет 60 км отправились одновременно в одном направлении лодка и катер.
Скорость катера 28 км/ ч , скорость лодки 8 км/ч .
Через некоторое время катер догнал лодку . Найди расстояние , пройденное катером.
Решение.
Скорость догона катера равна 28-8=20 км/час
S=vt;
60=20t;
t=3 часа
За 3 часа катер км.
***
2) Дано.
Из пункта А и В одновременно в одном направлении выехали два поезда . Скорость первого 80 км/ч , расстояние между пунктами 120 км . Найди скорость второго поезда, если первый поезд догонит второй через 4 часа.
Решение.
Пусть скорость второго поезда равна х км/час
Скорость догона равна 80 - х км/час.
S= vt;
120 = (80-x)4;
120=320-4x;
4x=320-120;
4x= 200;
х=50км/час скорость второго поезда