Первый игрок - Инна.
Пошаговое объяснение:
Вне зависимости от расстановки знаков в итоге значение выражения получится четным, поэтому всегда будет выигрывать первый игрок. Докажем это.
Будем рассматривать все возможные суммы из первых k чисел с произвольными знаками.
При k = 1 это {1}
При k = 2 это {1-2, 1+2} = {-1, 3}
При k = 3 это {-1-3, -1+3, 3-3, 3+3} = {-4, 0, 2, 6}
Видим, что четность чисел в множестве для фиксированных первых k одинаковая. Тогда очевидно, что если формировать множество для последовательности чисел длины k+1, то также получится множество с числами одинаковой четности. Объясняется это тем, что если взять конкретное число x, вычислить сумму и разность с некоторым y, то получатся два числа x-y и x+y одинаковой четности, так как (x+y) - (x-y) = 2y - четное.
Поэтому чтобы определить четность выражения из 100 элементов 1...100 с произвольными знаками, достаточно взять сумму с плюсами - она будет иметь ту же четность, что и любая другая сумма. (1+100)/2*100 = 5050 - четное число, поэтому побеждает всегда первый игрок.
Пошаговое объяснение:
Первоначальная дробь :

т.е первоначально числитель был 100 % , а когда его увеличили на 50% он стал :
100+50= 150 % или
150 : 100= 1,5 от первоначального
Число ,на которое надо уменьшить знаменатель , обозначим как у
Последующая дробь будет в 2 раза больше первоначальной , значит : 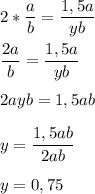
значит , первоначальный знаменатель надо уменьшить на 0,75
0,75 = 75 * 100 = 75 % - это процент , который составляет новый знаменатель от первоначального. Поскольку первоначальный знаменатель был 100 % , значит новый знаменатель был на
100 - 75 = 25 % меньше первоначального.
ответ : первоначальный знаменатель надо уменьшить на 25 % , чтоб получить дробь в 2 раза больше исходной
Пошаговое объяснение:
1) 6 × 3 = 18 компьютеров в большом зале
2) 6 + 18 = 24
ответ: всего 24 компьютеров