Пошаговое объяснение:
При решении задач на нахождение двух чисел по их сумме и разности схематические рисунки. Рассмотрим задачу. В одной корзине на восемь яблок больше, чем во второй. В двух корзинах вместе двадцать яблок. Сколько яблок в каждой корзине? Решение: выполним схематический рисунок. Покажем две корзины, в первой – на восемь яблок больше. Общее количество яблок двадцать. ... ответ: 988 см2. Опираясь на данные задачи, мы можем составить примерную схему решения задач на нахождение двух чисел по их сумме и разности: составляем схему по условию задачи; вычитаем из общей суммы лишнее (уравниваем количество); делим это количество поровну; отвечаем на вопрос задачи
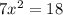, а квадратное. Посоветовал бы для начала умножить все части уравнения на –1, получив при этом уравнение вида 
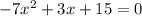, уже легче поддающееся решению. 
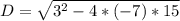, или равен 
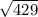, что в калькуляторе равно примерно 20,712... 
) расписывается следующим образом (конкретно для данного уравнения):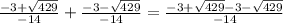 
и равна она, вообщем-то, шести четырнадцатым – обозначим её переменной α. Теперь же начертим числовую прямую, обозначив на ней α. 
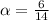, или равно 
. )∪(; +∞)
Наличие функции S(N) такой, что S(N) всегда принадлежит N (Для каждого элемента есть задать минимум один соседний элемент)
Отсутствие элементов, таких что S(N) = 1 (Для единичного ровно один)
Отсутствие элементов, таких что для элементов N1,N2 S(N1) = S(N2) (Для прочих не более двух, и этот однозначен для всех элементов N)
Отсутствие элементов, таких что зависящий от элемента N предикат P(N) ложен если P(1), P(N) и P(S(N)) истинны. (Прочие же свойства натуральных чисел одинаковы, какие бы натуральные числа мы не брали, и какие бы их свойства не исследовали