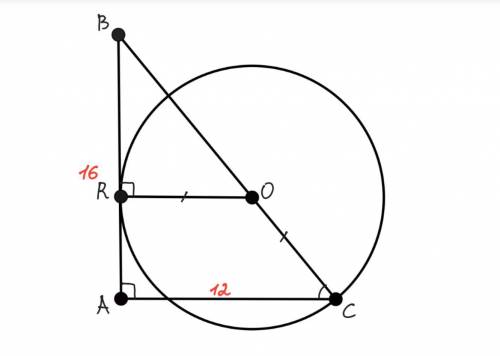
Дано: ΔABC — прямокутний, АВ і АС — катети, АВ=16 см, АС=12 см, коло(R;OC), т.О∈ВС, т.R — точка дотику кола до ΔАВС, т.R∈AB.
Знайти: радіус R кола.
Розв'язання.
1) Знайдемо гіпотенузу ВС ΔАВС за т.Піфагора:
АВ²+АС²=ВС²;
16²+12²=ВС²;
ВС²= 256+144;
ВС²= 400;
ВС= 20 см (–20 не задовольняє умові)
2) Проведемо радіус OR. R=OR=OC. Оскільки т.R — точка дотику, то OR⟂АВ.
3) Оскільки OR⟂AB і AB⟂AC (катети перпендикулярні), то OR||AC і трикутники ΔАВС і ΔRBO подібні за лемою.
(Лема про подібні трикутники: пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному)
4) ΔАВС подібний ΔRBO. Це означає, що відповідні сторони цих трикутників відносяться.
А тому справедливою буде така рівність:
АС/OR=BC/BO.
Нехай OR=OC=R (радіус, який потрібно знайти). Тоді ВО=ВС–ОС=ВС–R=20–R.
AC / R=BC / (BC–R);
12 / R= 20 / (20–R); (по пропорции решаем)
12(20–R)=20R;
240–12R=20R;
240=32R;
R= 240/32;
R= 15/2;
R= 7,5 (см)
Відповідь: 7,5 см.
ответ Б.
Арина.
Пошаговое объяснение:
Сначала нам нужно разбить это число на нужные числа, которые соответствуют порядковым номерам букв.
В русском алфавите 33 буквы, то есть числа могут быть от 1 до 33.
Обратим внимание на конец шифровки. Последние цифры 51.Так как букв 33, то буквы с номером 51 нет. То есть последняя буква под номером 1.
Посмотрим на середину. Там есть 0. Так как нет буквы с порядковым номером 0, то к этому числу поставляем соседнюю левую цифру и получаем 10.
Сейчас получили:
118 10 15 1
Заметим, что 118 можно поделить так: 1 и 18, или так: 11 и 8.
15 можно использовать как значение под букву или разделить как 1 и 5.
Поэтому вариантов 4:
1 18 10 15 1
11 8 10 15 1
1 18 10 1 5 1
11 8 10 1 5 1
Подставим буквы:
1- А
5- Д
8- Ж
10- И
11- Й
15- Н
18- Р
1 18 10 15 1- АРИНА
11 8 10 15 1- ЙЖИНА
1 18 10 1 5 1- АРИАДА
11 8 10 1 5 1- ЙЖИАДА
В данном случае, имеет место быть только одно имя- Арина.
2) 4*3=12 (км) -
3) 72-12=60 (км)
ответ: 60 км