-5 < a < -1/2 или 3 < a < 7/2
Пошаговое объяснение:
Сделаем замену x + 4/x = y. Получается квадратное уравнение:
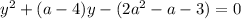
Домножим на 4 и выделим полный квадрат. Получится разность квадратов, которую преобразуем в произведение:
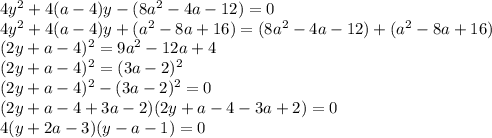
Если вам не нравится такой можете использовать дискриминант или угадать корни, пользуясь теоремой Виета. Так или иначе, корни этого уравнения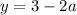 
и 
.
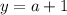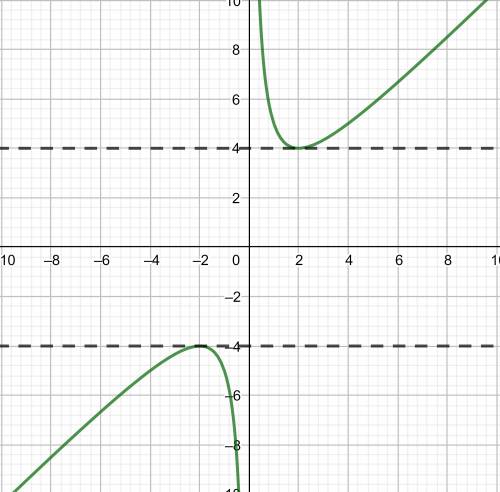
Когда мы вернемся обратно к иксам, нужно будет определять количество корней уравнения вида x + 4/x = t. Нарисуем график функции f(x) = x + 4/x. Это нечетная функция, сфокусируемся на x > 0.
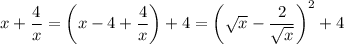
Минимальное значение f(x) равно 4, достигается при x = 2. При x > 2 функция неограниченно возрастает (поскольку выражение в скобках положительно и оба слагаемых возрастают), а так как уравнение переходит само в себя при замене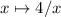 
, то при 0 < x < 2 функция убывает от бесконечности.
При x < 0 всё получается симметрично относительно начала координат. График показан на картинке.
Итак, x + 4/x = t не имеет решений, если -4 < t < 4, одно решение, если t = -4 или t = 4, и два решения во всех остальных случаях.
Осталось понять, когда у исходного уравнения будет два решения.
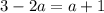и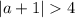 
Первое равенство выполнено при a = 2/3, тогда у уравнения нет решений. Не подходит
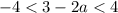и 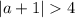Первое неравенство дает -1/2 < a < 7/2, второе a > 3 или a < -5. Пересечение: 3 < a < 7/2.
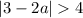и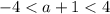 
Первое неравенство: a > 7/2 или a < -1/2, второе: -5 < a < 3. Пересечение: -5 < a < -1/2.
3 - 2a = 4, a + 1 = -4Нет решений
3 - 2a = -4, a + 1 = 4Нет решений
а) Запишем уравнение в следующем виде: tg(x)dy(x)/dy-y(x)=2
dy(x)/dy=(2-y(x))*ctg(x)
Делим обе части на (2-y(x)):
(dy(x)/dy)/(2-y(x))=ctg(x)
Интегрируем обе части по Х:
инт((dy(x)/dy)/(2-y(x)))=инт(ctg(x)dx)
Получаем: lg(y+2)=lg(sinx)+C1
Т.к. lg(y+2)-lg(sinx)=lg((y+2)/sin(x)), то lg((y+2)/sin(x))=С1
(y+2)/sin(x)=е^C1
y=C1*(sin(x)-2)
б) Запишем характеристическое уравнение: 3*k^2-2*k-8=0
Корни этого уравнения k1=(2-корень(2^2-4*3*(-8)))/(2*3)=-8/6=-4/3
k2=(2+корень(2^2-4*3*(-8)))/(2*3)=2
Решение данного уравнения будет иметь вид e^k*x.
Общее решение: y=e^(-4*x/3)*C1+e^(2x/)*C2
