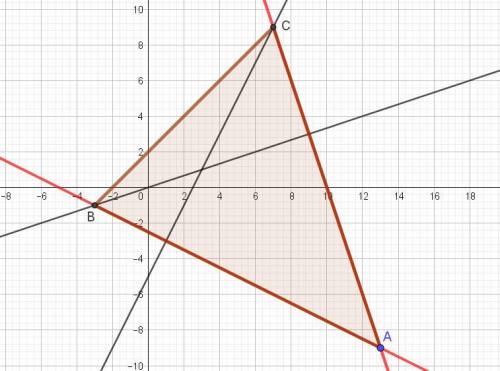
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
Двухгранный угол между плоскостями равен линейному углу АОВ = 1200.
Из точки М проведем перпендикуляры к ОА и ОВ, а так же соединим точку М и О.
Треугольники АОМ и ВОМ прямоугольные, у которых гипотенуза ОМ общая, а катеты АМ и ВМ, во условию равны, тогда прямоугольные треугольники АОМ и ВОМ равны по катету и гипотенузе, четвертому признаку равенства прямоугольных треугольником.
Тогда углы АОМ и ВОМ равны, а ОМ биссектриса угла АОВ, тогда угол АОВ = ВОМ = 600.
В прямоугольном треугольнике ВОМ Sin60 = ВМ / ОМ.
ОМ = BM / Sin60 = m / (√3 / 2) = 2 * m /√3 = 2 * m * √3 / 3 см.
ответ: От точки М до ребра двухгранного угла 2 * m * √3 / 3 см.
14/2= 7 яблок на каждой тарелке
7+2=9 яблок на первой тарелке
7-3=4 яблока на второй тарелке