Вычисли 210+60 на какие числа от 1 до 10 можно разделить результ вычислений

👇

Увидеть ответ

Ответ:

амина11

25.02.2021

210+60=270
Будет делится на 10,2,4

4,7(31 оценок)

Открыть все ответы

Ответ:

Аббос1111

25.02.2021

Даны координаты вершин пирамиды:
А(0; 1; -1), B(-2; 3; 5), C(1; -5; -9), D(-1 ;-6; 3).

1) Определяем уравнение плоскости BCD:
Уравнение плоскости:
A · x + B · y + C · z + D = 0 .
Для нахождения коэффициентов A, B, C и D нужно решить систему:
A · x1 + B · y1 + C · z1 + D = 0 ,
A · x2 + B · y2 + C · z2 + D = 0 ,
A · x3 + B · y3 + C · z3 + D = 0 .
Решим эту систему, которая в нашем случае запишется следующим образом:
A · (-2) + B · (3) + C · (5) + D = 0 ,
A · (1) + B · (-5) + C · (-9) + D = 0 ,
A · (-1) + B · (-6) + C · (3) + D = 0 .
Решение матричным

(x - (-2))-(8·(-2)-(-14)·(-9)) - (y - 3)(3·(-2)-(-14)·1) + (z - 5)(3·(-9)-(-8)·1) = 0

(-110)(x - (-2)) + (-8)(y - 3) + (-19)(z - 5) = 0

- 110x - 8y - 19z - 101 = 0.

Если умножим на -1, то получим уравнение плоскости:

110 · x + 8 · y + 19 · z + 101 = 0 .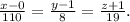
Координаты точки А: (0; 1; -1).
Если прямая перпендикулярна плоскости 110x + 8y + 19z + 101 = 0, значит она параллельна нормальному вектору этой плоскости n⃗ ={110; 8; 19}. Итак надo составит уравнение прямой с направляющим вектором n⃗ , проходящей через точку А (0; 1; -1).
$\frac{x-0}{110} = \frac{y-1}{8}= \frac{z+1}{19} .$

2) Расстояние от точки А до плоскости BCD.
Для вычисления расстояния от точки А(0, 1, -1) до плоскости
110x + 8y + 19z + 101 = 0 используем формулу:

d = |A·Аx + B·Ау + C·Аz + D|/√(A² + B² + C²).
Подставим в формулу данныеd = |110·0 + 8·1 + 19·(-1) + 101|/√(110² + 8² + 19²) =
= |0 + 8 - 19+ + 101| / √(12100 + 64 + 361) =
= 90/√12525 = 6√501/167 ≈ 0,80418069.

3) Угол между прямой АС и плоскостью BCD.
Уравнение АС: (x-0)/1 = (y-1)/(-6) = (z+1)/(-8).

Направляющий вектор прямой имеет вид:s = 1; -6; -8

Вектор нормали плоскости имеет вид:q = 110; 8; 19

Угол между прямой и плоскостью: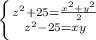
sin φ = | A · l + B · m + C · n | /(√A² + B² + C² · √l² + m² + n²) =
= | 110 · 1 + 8 · (-6) + 19 · (-8) | /(√110² + 8² + 19² · √1² + (-6)² + (-8)²) =
= | 110 - 48 - 152 | /(√(12100 + 64 + 361)·√(1 + 36 + 64)) =
= 90 /(√12525·√101) = 90/√1265025 = 6√50601/16867 ≈ 0,0800189697.
Этому синусу соответствует угол 0,0801046 радиан или 4,5896561°.

4,4(15 оценок)

Ответ:

Witch23

25.02.2021

Дана система уравнений:
{x² + y² - 2z² = 50    (1)
{x + y + 2z = 104        (2)
{z² - xy = 25.    (3)

Выразим z² их уравнения (3) и подставим в уравнение (1).
x² + y² - 2 xy - 50 = 50.
Выделим полный квадрат:
x² - 2xy + y² = 100.
(x - y)² = 100.
x - y = +-10.
Отсюда видно, что значения х и у могут иметь по 2 значения:
х - у = 10,          (4)
-х + у = 10. (5)
В уравнении (1) разделим обе части на 2 и вместе с уравнением (3) запишем так:
$\left \{ {{z^2+25= \frac{x^2+y^2}{2} } \atop {z^2-25=xy}} \right.$
Сложим эти 2 уравнения и приведём к общему знаменателю:
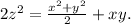
$2z^2= \frac{x^2+y^2}{2}+xy.$
4z² = x² + y² +2xy.
4z² = (x + y)².
Извлечём корень: 2z = х + у.    (6)
Из уравнения (2) имеем 2z = 104 - (х + у) и значение 2z подставим в уравнение (6): 104 - (х + у) = х + у.
Отсюда имеем 2(х + у) = 104,
   х + у = 104/2 = 52. (7)
Теперь, сопоставив уравнения (4), (5) и (7), получаем значения х и у:
{ х - у = 10,            (4)
{ х + у = 52. (7)
----------------
2x = 62 x= 62/2 =  31, y = x - 10 = 31 - 10 =21.


{ -х + у = 10,            (5)
{ х + у = 52.    (7)
----------------
    2y = 62 y= 62/2 =  31, x = y - 10 = 31 - 10 =21.
Значение z получится одно:
z = (x + y)/2 = 52/2 = 26.

В соответствии с заданием получается 2 ответа:
1) Если решений несколько, выберите то, в котором x принимает наибольшее значение. В ответ впишите значение величины
10000x+100y+z = 310000+2100+26 = 312126.
2) 10000x+100y+z = 210000+3100+26 =  213126.

4,5(100 оценок)

Это интересно:

Здоровье

28.05.2020

Как быстро набрать вес (для женщины): советы и рекомендации...

Дом-и-сад

10.01.2021

Как избавиться от беспорядка на кухонной полке: Правильный способ сделать подкладку...

Здоровье

02.11.2021

Как распознать разрушение зубной эмали...

Здоровье