Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
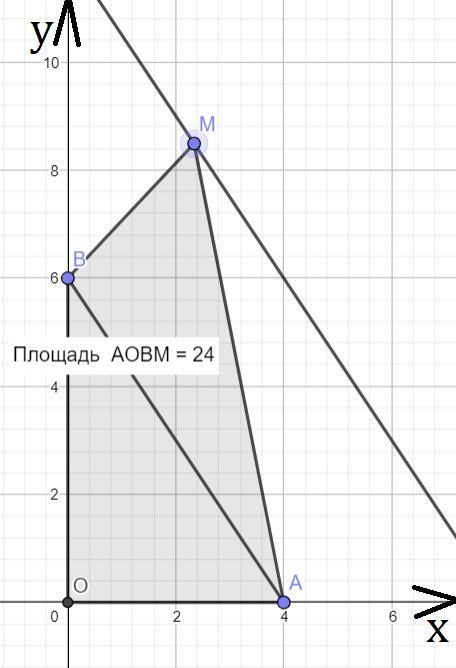
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
ответ: y= -1,5; 8
( 12 у + 18) (1,6 – 0,2у) = 0.
Нулем ( ноль произведением является тогда, когда хотя бы один множитель- 0) является либо первая часть уравнения, либо вторая, либо обе они одновременно.
Предположим, что первая часть=0
Тогда 12y должны быть равны -18 (18+(-18)=0),
Тогда у = -18:12= -1,5
Подставляем значение у во вторую часть уравнения
1,6 - 0,2*(-1,5)= 1,6 - (-0,3)= 1,9
1,9 не равно 0, значит обе части уравнения нулем не являются.
Ну и разбираем последний вариант, когда 1,6 - 0,2у=0;
Тогда 0,2у должен равнятся 1,6 ( 1,6:0,2= 8)
Тогда у =8
ответ:
пошаговое объяснение:
an+1 = an + d где d – это разность арифметической прогрессии. пример: последовательность чисел 3, 7, 11, 15, 19, является арифметической прогрессией с разностью d = 4. арифметическая прогрессия бывает трех видов: возрастающая — арифметическая прогрессия, у которой разность является положительной пример: последовательность чисел 2, 5, 8, 11, 14, является возрастающей арифметической прогрессией, так как ее разность d = 3. убывающая — арифметическая прогрессия, у которой разность является отрицательной пример: последовательность чисел 100, 98, 96, 94, 92, является убывающей арифметической прогрессией, так как ее разность d = –2. стационарная — арифметическая прогрессия, у которой разность равно нулю пример: последовательность чисел 23, 23, 23, 23, 23, является стационарной арифметической прогрессией, так как ее разность d = 0.