V=64π кубических единиц объем искомого конуса.
Пошаговое объяснение:
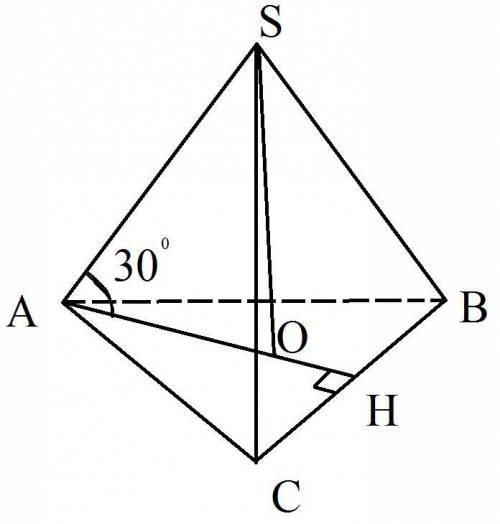
Рисунок смотрите в приложении.
Объем конуса вычисляется по формуле
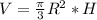 (*).
(*).
Здесь R - радиус основания конуса, Н - высота конуса.
Найдем радиус основания конуса. Он равен радиусу описанной окружности основания пирамиды.
SO - высота конуса. Точка О - центр вписанной и описанной окружности правильного треугольника.
АО=R - длина радиуса описанной окружности.
Радиус описанной окружности вычисляется по формуле
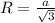 , где а - это длина стороны треугольника.
, где а - это длина стороны треугольника.
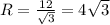 единиц.
единиц.
Из ΔАОS, который по построению прямоугольный (∠О=90°), по условию задачи ∠SAO=30°. Так как это и есть угол между ребром и основанием пирамиды. Теперь из этого треугольника можно найти SO. SO=AO*tg∠SAO. SO=AO*tg30°,
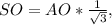
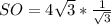 ,
,
SO=4 единицы.
Подставим в формулу (*).
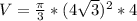 ,
,
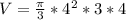
V=π*4³ кубических единиц.
V=64π кубических единиц.
Пошаговое объяснение:
Чтобы понять этот момент, сначала надо разобраться с тем, что такое (x+y)^2
(x+y)^2=(x+y)(x+y)=x^2+xy+xy+y^2=x^2+2xy+y^2
Это довольно известная формула, проходится в школе и наверняка у тебя она была, это то, как раскрывается квадрат суммы двух слагаемых
Теперь, когда мы понимаем как раскрывается квадрат суммы двух слагаемых, можем ли мы понять как раскрывается квадрат суммы трех слагаемых?
То есть, еще раз, мы знаем что делать если слагаемых два (x+y)^2=x^2+2xy+y^2
А что делать если слагаемых три?
(a+b+c)^2=???
Можно попробовать применить хитрый ход и рассмотреть выражение a+b как одно слагаемое
Если это тяжело для понимания, то просто представь как будто ты сделала замену a+b=x; c=y
Тогда твое выражение (a+b+c)^2 превращается в (x+y)^2 и ты уже знаешь что с ним делать
У тебя (x+y)^2=x^2+2xy+y^2, после того как мы сделаем обратную замену (заменим x на a+b; y на c), получим следующую запись:
(a+b)^2+2(a+b)c+c^2
Пойдем дальше
(a+b)^2=a^2+2ab+b^2 (аналогично)
2(a+b)c=2ac+2bc
Итого
a^2+2ab+b^2+2ac+2bc+c^2, то что у них получилось в конце
21l3 14l2
7l7 7l7
1. 1
3*2*7*2*3=168