Если отношение первой цифры ко второй цифре равно 4: 7, сколько будет вторая цифра к первой?

👇

Увидеть ответ

Открыть все ответы

Ответ:

nasamar

21.08.2022

$\mathrm{tg}a_1\mathrm{tg}a_2+\mathrm{tg}a_2\mathrm{tg}a_3+\mathrm{tg}a_3\mathrm{tg}a_4+\mathrm{tg}a_4\mathrm{tg}a_5=4$

Выразим через третий член и разность прогрессии все остальные члены:

a_1=a_3-2d

a_2=a_3-d

a_4=a_3+d

a_5=a_3+2d

Подставим получившиеся соотношения в уравнение:

$\mathrm{tg}(a_3-2d)\cdot\mathrm{tg}(a_3-d)+\mathrm{tg}(a_3-d)\cdot\mathrm{tg}a_3+$

$+\mathrm{tg}a_3\cdot\mathrm{tg}(a_3+d)+\mathrm{tg}(a_3+d)\cdot\mathrm{tg}(a_3+2d)=4$

Применяем формулы тангенса суммы и тангенса разности:

$\dfrac{\mathrm{tg}a_3-\mathrm{tg}2d}{1+\mathrm{tg}a_3\mathrm{tg}2d}\cdot\dfrac{\mathrm{tg}a_3-\mathrm{tg}d}{1+\mathrm{tg}a_3\mathrm{tg}d}+\dfrac{\mathrm{tg}a_3-\mathrm{tg}d}{1+\mathrm{tg}a_3\mathrm{tg}d}\cdot\mathrm{tg}a_3+$

$+\mathrm{tg}a_3\cdot\dfrac{\mathrm{tg}a_3+\mathrm{tg}d}{1-\mathrm{tg}a_3\mathrm{tg}d}+\dfrac{\mathrm{tg}a_3+\mathrm{tg}d}{1-\mathrm{tg}a_3\mathrm{tg}d}\cdot\dfrac{\mathrm{tg}a_3+\mathrm{tg}2d}{1-\mathrm{tg}a_3\mathrm{tg}2d}=4$

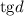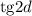Из имеющегося соотношения для разности прогрессии выразим величины $\mathrm{tg}d$ и $\mathrm{tg}2d$ :

$\cos d=\sqrt{0.2}$

$\mathrm{tg}^2d=\dfrac{1}{\cos^2d} -1=\dfrac{1}{0.2} -1=5-1=4$

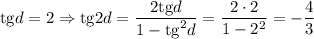
1) $\mathrm{tg}d=2\Rightarrow \mathrm{tg}2d=\dfrac{2\mathrm{tg}d}{1-\mathrm{tg}^2d} =\dfrac{2\cdot2}{1-2^2} =-\dfrac{4}{3}$

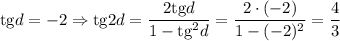
2) $\mathrm{tg}d=-2\Rightarrow \mathrm{tg}2d=\dfrac{2\mathrm{tg}d}{1-\mathrm{tg}^2d} =\dfrac{2\cdot(-2)}{1-(-2)^2} =\dfrac{4}{3}$

Первый случай: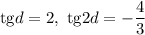 $\mathrm{tg}d=2,\ \mathrm{tg}2d=-\dfrac{4}{3}$

$\dfrac{\mathrm{tg}a_3+\frac{4}{3} }{1-\frac{4}{3}\mathrm{tg}a_3}\cdot\dfrac{\mathrm{tg}a_3-2}{1+2\mathrm{tg}a_3}+\dfrac{\mathrm{tg}a_3-2}{1+2\mathrm{tg}a_3}\cdot\mathrm{tg}a_3+$

$+\mathrm{tg}a_3\cdot\dfrac{\mathrm{tg}a_3+2}{1-2\mathrm{tg}a_3}+\dfrac{\mathrm{tg}a_3+2}{1-2\mathrm{tg}a_3}\cdot\dfrac{\mathrm{tg}a_3+\frac{4}{3} }{1-\frac{4}{3}\mathrm{tg}a_3}=4$

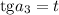
Замена: $\mathrm{tg}a_3=t$

$\dfrac{t+\frac{4}{3} }{1-\frac{4}{3}t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t+t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{t-\frac{4}{3} }{1+\frac{4}{3}t}=4$

Числитель и знаменатель первой и последней дроби умножим на 3:

$\dfrac{3t+4 }{3-4t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t+t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{3t-4}{3+4t}=4$

Складываем первые два слагаемых левой части уравнения:

$\dfrac{3t+4}{3-4t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t=\dfrac{t-2}{1+2t}\cdot\left(\dfrac{3t+4}{3-4t}+t\right)=$

$=\dfrac{t-2}{1+2t}\cdot\dfrac{3t+4+t(3-4t)}{3-4t}=\dfrac{t-2}{1+2t}\cdot\dfrac{3t+4+3t-4t^2}{3-4t}=$

$=\dfrac{t-2}{1+2t}\cdot\dfrac{4+6t-4t^2}{3-4t}=\dfrac{t-2}{1+2t}\cdot\dfrac{-2(t-2)(2t+1)}{3-4t}=$

$=\dfrac{-2(t-2)^2(2t+1)}{(1+2t)(3-4t)}=-\dfrac{2(t-2)^2}{3-4t}$

Складываем последние два слагаемых левой части уравнения:

$t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{3t-4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\left(t+\dfrac{3t-4}{3+4t}\right)=$

$=\dfrac{t+2}{1-2t}\cdot\dfrac{t(3+4t)+3t+4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\dfrac{3t+4t^2+3t+4}{3+4t}=$

$=\dfrac{t+2}{1-2t}\cdot\dfrac{4t^2+6t+4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\dfrac{2(t+2)(2t-1)}{3+4t}=$

$=\dfrac{2(t+2)^2(2t-1)}{(1-2t)(3+4t)}=-\dfrac{2(t+2)^2}{3+4t}$

Складываем две получившиеся в предыдущих пунктах величины:

$-\dfrac{2(t-2)^2}{3-4t}-\dfrac{2(t+2)^2}{3+4t}=-2\left(\dfrac{(t-2)^2}{3-4t}+\dfrac{(t+2)^2}{3+4t}\right)=$

$=-2\left(\dfrac{t^2-4t+4}{3-4t}+\dfrac{t^2+4t+4}{3+4t}\right)=$

$=-2\left(\dfrac{(t^2-4t+4)(3+4t)+(t^2+4t+4)(3-4t)}{(3-4t)(3+4t)}\right)=$

$=-2\left(\dfrac{3t^2+4t^3-12t-16t^2+12+16t+3t^2-4t^3+12t-16t^2+12-16t}{9-16t^2}\right)=$

$=-2\left(\dfrac{3t^2-16t^2+12+3t^2-16t^2+12}{9-16t^2}\right)=-2\left(\dfrac{-26t^2+24}{9-16t^2}\right)=\dfrac{52t^2-48}{9-16t^2}$

Тогда, уравнение примет вид:

$\dfrac{52t^2-48}{9-16t^2}=4$

52t^2-48=4(9-16t^2)

52t^2-48=36-64t^2

116t^2=84

$t^2=\dfrac{84}{116} =\dfrac{21}{29}$

$t=\pm\sqrt{\dfrac{21}{29} }$

Обратная замена: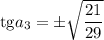 $\mathrm{tg}a_3=\pm\sqrt{\dfrac{21}{29} }$

Находим требуемую величину:

$\cos^2 a_3=\dfrac{1}{1+\mathrm{tg}^2a_3} =\dfrac{1}{1+\frac{21}{29} } =\dfrac{1}{\frac{50}{29} } =\dfrac{29}{50} =\boxed{0.58}$

Второй случай: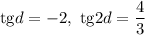 $\mathrm{tg}d=-2,\ \mathrm{tg}2d=\dfrac{4}{3}$

Заметим, что при подстановке этих значений в уравнение, получится такое же уравнение, как и в предыдущем случае с той лишь разницей, что первое и четвертое, а также второе и третье слагаемое будут поменяны местами. Значит, никаких новых результатов получено не будет.

ответ: 0.58

4,7(47 оценок)

Ответ: