Введите поисковой запрос
Расширенный поиск
ВОЙТИ / ЗАРЕГИСТРИРОВАТЬСЯЕдиное окно доступа к образовательным ресурсам
ДИСКРЕТНАЯ МАТЕМАТИКА: МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО КУРСУ
Автор/создатель: Азарнова Т.В., Булгакова И.Н.
13
Голосов: 12
Данная работа содержит краткое изложение теории множеств, бинарных отношений и комбинаторики, соответствующее курсу лекций по дисциплине "Дискретная математика", читаемому на факультете ПММ. Пособие содержит ряд примеров, демонстрирующих использование изложенной теории для решения конкретных задач. Для закрепления материала в конце параграфов приведены задачи для самостоятельного решения, которые могут быть также использованы для проведения практических занятий.
Приведенный ниже текст получен путем автоматического извлечения из оригинального PDF-документа и предназначен для предварительного просмотра.
Изображения (картинки, формулы, графики) отсутствуют.
Страницы ← предыдущая следующая →
1 2 3 4 5 6
11
Теория множеств
1) последовательности непустых множеств Χ 1 , Χ 2 ,..., Χ n ,..., такой, что
Χ 1 ⊃ Χ 2 ⊃ ... и Ι Χ n = ∅ ;
n∈Ν
2) последовательности множеств, отличных от универсального множества
Λ , такой, что Χ 1 ⊂ Χ 2 ⊂ ... и Υ Χ n = Λ ;
n∈Ν
3) семейства множеств такого, что пересечение любого конечного числа
множеств из этого семейства непусто, а пересечение всех множеств пусто.
§ 2. Прямое произведение множеств.
Бинарные отношения
Произведением (или декартовым произведением) Χ 1 × Χ 2 двух
непустых множеств Χ 1 и Χ 2 будем называть множество упорядоченных
пар (x1 , x 2 ), где x1 ∈ Χ 1 , x 2 ∈ Χ 2 . Это понятие выросло из понятия
декартовой системы координат. Данное понятие можно обобщить и на
случай n множеств. Если Χ 1 , Χ 2 ,..., Χ n - n непустых множеств, то их
произведение состоит из всевозможных упорядоченных наборов
(x1 , x 2 ,..., x n ) , x k ∈ Χ k , k = 1,..., n элементов этих множеств. Если множества
Χ 1 = Χ 2 = ... = Χ n = Χ , то их произведение Χ 1 , Χ 2 ,..., Χ n обозначается
Χ n . Так, символом R n обозначается множество упорядоченных векторов n
вещественных чисел.
Любое подмножество из произведения Χ ×Υ называется бинарным
отношением. Если Χ =Υ , то бинарное отношение называется бинарным
отношением на множестве Χ . Бинарные отношения обозначаются буквами
φ , ρ , f ,... Если пара (x, y ) принадлежит бинарному отношению ρ , то пишут
(x, y )∈ ρ или x ρ y .
Для задания бинарного отношения ρ используют те же методы, что и
для произвольных множеств, кроме того, бинарное отношение, заданное на
конечном множестве Χ , можно задать в виде графа, а бинарное отношение
на множестве R можно задать в виде декартовой диаграммы. Под графом
бинарного отношения мы понимаем схему, в которой элементы множества
Χ изображаются точками на плоскости, элементы x, y ∈ Χ , такие, что пара
(x, y )∈ ρ соединяются стрелкой, направленной от x к y , пары (x, x )∈ ρ
изображаются петлей вокруг точки x . Под декартовой диаграммой
понимают изображение пар (x, y ) ∈ ρ в декартовой прямоугольной системе
координат.
Областью определения бинарного отношения ρ называется множество
D ρ = {x ∈ Χ : ∃y (x, y )∈ ρ }.
Областью значений бинарного отношения ρ называется множество
R ρ = {y ∈Υ : ∃x (x, y )∈ ρ }.
12
Теория множеств
Бинарное отношение ρ на множестве Χ называется рефлексивным,
если для любого x ∈ Χ пара (x, x ) ∈ ρ . Если Χ - конечное множество, то
рефлексивность бинарного отношения ρ означает, что на графе данного
бинарного отношения вокруг каждой точки x из Χ есть петля. Если Χ = R ,
то рефлексивность бинарного отношения ρ с точки зрения декартовой
диаграммы означает, что в число изображенных точек войдут все точки
прямой y ( x) = x .
Бинарное отношение ρ на (4,2 ), .
(2,3), (2,4), (2,5) (5,1), (5,2)
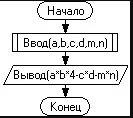
Алгоритм:
1) Узнать площадь всех стен комнаты. (S₁=a*b*4)
2) Узнать суммарную площадь окна и двери. (S₂=c*d+m*n)
3) Вычесть от всей площади суммарную площадь окна и двери. (S=S₁-S₂)
Блок-схема в приложении
Код PascalABC:
var
a, b, c, d, m, n: integer;
begin
readln(a, b, c, d, m, n);
writeln(a * b * 4 - (c * d + m * n));
end.
номер 2
1 байт = 8 бит
1 Кб (1 Килобайт) = 210 байт = 2*2*2*2*2*2*2*2*2*2 байт =
= 1024 байт (примерно 1 тысяча байт – 103 байт)
1 Мб (1 Мегабайт) = 220 байт = 1024 килобайт (примерно 1 миллион байт – 106 байт)
1 Гб (1 Гигабайт) = 230 байт = 1024 мегабайт (примерно 1 миллиард байт – 109 байт)
1/3х-засолили вначале
1/2х-осталось засолить
Составим уравнение:
1/3х+1,5+1/2х=х
1,5=х-1/3х-1/2х
1,5=1/6х
1/6х=1,5
х=15/10 ÷ 1/6
х=9
ответ: 9