Question

Востроугольном треугольнике авс точка м -середина стороны ав, аа1и вв1 -высоты .докажете ,что треугольник а1мв1-равнобедренный , и найдите его периметр , если ав =6 и cosc =2/3

Answer 1

∠AA₁B и ∠AB₁B равны и опираются на один и тот же отрезок, значит, точки A, B, A₁, B₁ лежат на одной окружности. ∠AA₁B = 90° ⇒ AB — диаметр. Так как AM = MB, M — центр окружности ⇒ MA₁ и MB₁ — радиусы ⇒ A₁M = B₁M ⇒ ΔA₁MB₁ — равнобедренный.

P = A₁M + B₁M + A₁B₁. A₁M = B₁M = R = AB/2 = 3.

В прямоугольном ΔAA₁C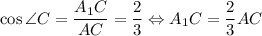 $\cos{\angle C}=\dfrac{A_1C}{AC}=\dfrac{2}{3}\Leftrightarrow A_1C=\dfrac{2}{3}AC$

В прямоугольном ΔBB₁C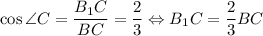 $\cos{\angle C}=\dfrac{B_1C}{BC}=\dfrac{2}{3}\Leftrightarrow B_1C=\dfrac{2}{3}BC$

Рассмотрим ΔA₁B₁C и ΔABC:

∠C — общий;$A_1C=\dfrac{2}{3}AC;$ ⇒$B_1C=\dfrac{2}{3}BC;$

⇒ ΔA₁B₁C ~ ΔABC по углу и двум пропорциональным сторонам ⇒ $A_1B_1=\dfrac{2}{3}AB=4$

P = 3 + 3 + 4 = 10

ответ: 10