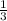
Пошаговое объяснение:
Чтобы дробь достигала минимального значения, числитель должен быть минимален, а знаменатель - максимальным. Заметим, что как в числителе, так и в знаменателе квадратные уравнения относительно a и b, причем в уравнении относительно a, минимальное значение которого нас интересует, коэффициент возле x² больше нуля, следовательно, ветки параболы направлены вверх, и минимальное значение функция принимает в вершине параболы.
В уравнении относительно b ветки параболы направлены вниз, следовательно, максимальное значение достигается так же в вершине параболы.
Вычислим абсциссы вершин парабол по формуле x=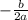
, где a и b - коэффициенты перед x² и x соответственно.
Абсцисса вершины параболы для функции относительно a x=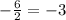
.
Значение ординаты в этой точке найдём, подставив полученное значение x в уравнение, получим:
y=9-18+16=7
Проделаем то же для уравнения в знаменателе, получим:
x=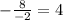
y=5+32-16=21
Минимальное положительное значение дроби: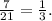 
16 операций
Пошаговое объяснение:
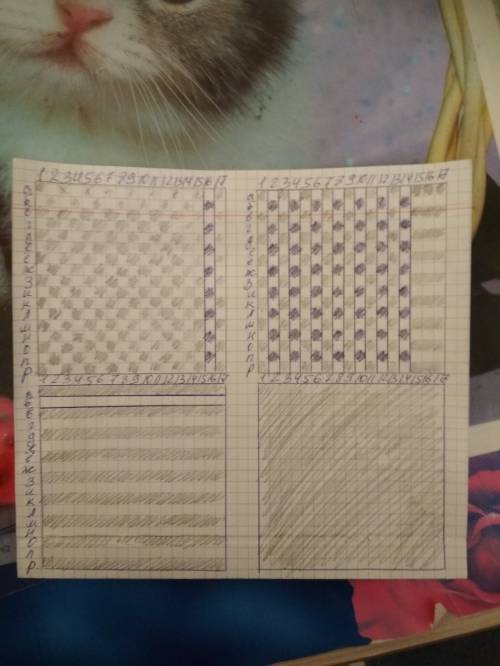
см. рисунок (алые розы - темные клетки, белые розы - белые клетки)
1) нарисуем квадрат 17х17 и закрасим клетки в шахматном порядке
Для удобства, пронумеруем столбцы и строки
2) в столбцах 16,14,12,10,8,6,4,2 так же поменяем цвета клеток на противоположные
Итого: получилось 9 строк алых роз (темные клетки) и 8 строк белых роз
Сделано 8 операций
3) теперь все строки белых роз (8 шт) превращаем в алые розы
Итого: во всех клетках квадрата лежат алые розы
Сделано 8+8=16 операций
ответ : 16 операций
12 это вместе Толя И Коля
А остальные 12 Папа
12:2=6
6 КОЛЯ
6 ТОЛЯ