7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть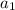 
- изначальное число и 
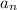- сумма цифр числа 
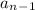. Пусть остаток при делении на 9 у числа 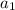- r, тогда и у числа 
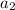остаток при делении на 9 тоже r. Но тогда и у чисел 
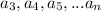остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа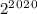 
. А он такой же, как у числа 
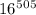, и такой же, как у числа 
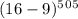, и такой же, как у числа 
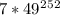, а он такой же, как у числа 
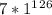, а это равно 7.
1. 24 : 3 = 8 (ч.) Он тратит на учебу.
Переходим к игре в футбол, находя ее продолжительность тем же
2. 24 : 4 = 6 (ч.) Уходит на игру в футбол.
Тем же находим остальные значения.
3. 24 : 5 = 4.8 (ч.) На прослушивание дисков.
4. 24 : 6 = 4 (ч.) На компьютер.
5. 24 : 7 = 3 3/7 (ч.) На решение задач по математике.
Теперь суммируются числа.
6. 8 + 6 + 4.8 + 4 + 3 3/7
Даже если брать в учет только целые числа, получается 25, что противеречит задаче, ведь он должен был уложится в 24. Значит, такой расход времени невозможен.
P.S. И вопрос к этой задаче очень напоминает философию :)