1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
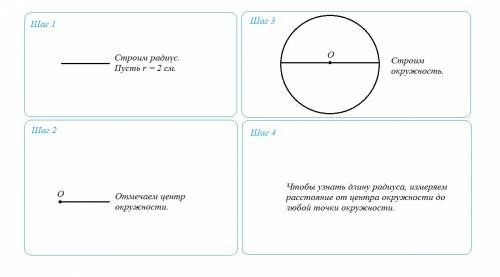
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.
ответ: У этих игр очень простая стратегия. Запомните её один раз и будете решать любые подобные задачи.
Пусть дано P предметов и за ход можно брать от 1 до n предметов.
Вычисляем "магическое число" М = n+1.
Находим остаток целочисленного деления P на M - он покажет, сколько спичек надо взять при первом ходе для выигрыша. Если 0 - то игрок, делающий ход первым, проигрывает. Выигрышная стратегия проста. Если противник взял k предметов, мы берем M-k.
Рассмотрим задачу 1.
P=25, n=4
М=n+1=5, P/M дает в остатке 0 - игрок, делающий ход первым, проигрывает.
Выигрышная стратегия: брать 5-k предметов, оставляя противнику 20, 15, 10 и 5 предметов.
Рассмотрим задачу 2.
P=107, n=2
M=n+1=3, P/M дает в остатке 2 - игрок, делающий ход первым, берет 2 предмета и выигрывает.
Выигрышная стратегия: брать 3-k предметов, оставляя противнику 105, 102, 99, 96, ... предметов.
Пошаговое объяснение:
1.) 200 - 50*3=200-150=50 л (осталось)
Делим оставшееся количество сока на маленькие банки
2.) 50:25=2 л
ответ: емкость маленькой банки - 2 литра