1. В гимназии, где учился Лобачевский, его недолюбливали. Мальчик пристрастился к пиротехническим опытам, за что даже однажды попал в карцер. Преподавателям не нравилось «мечтательное о себе самомнение, излишнее упорство и вольнодумствие» ученика. Несмотря на все это, Николай отлично учился.
2. Плохое поведение в гимназии чуть не сыграло злую шутку с Лобачевским. Он имел все шансы попасть в армию. Это могло произойти, когда вышел указ, предписывающий отдавать на службу тех студентов, которые отличались дурным поведением.
3. Лобачевского можно назвать юным гением. Уже в 19 лет он получил степень магистра, в 22 - адъюнкта чистой математики, а в 24 года был удостоен профессорского звания.
4. Ученый любил ухаживать за растениями в саду. Его «любимцами» были кедры. Однако Лобачевский говорил, что не дождется их плодов. Так и случилось. Они были сняты всего через несколько месяцев после смерти ученого.
5. Лобачевский отличился не только в точных науках, но также внедрял различные новшества в сельском хозяйстве. За некоторые достижения на этом поприще даже получал награды.
6. Труды Лобачевского не забыты до сих пор, а его талант не подлежит сомнению. Однако сам ученый боялся, что его труды забудут после смерти. Эти опасения подогревала интенсивная критика его работ. Умирая, он произнес с горечью: «И человек родился, чтобы умереть».
7. Лобачевский прекрасно владел даром убеждения. Он даже наставил на путь истинный одного из своих студентов. Парень любил выпить и даже бросался на людей с ножом, Лобачевский утихомирил лишь спокойным разговором. Кстати, с другими студентами у ученого тоже были теплые отношения. Он любил весело провести время с учениками, но панибратства никогда не допускал.
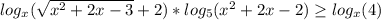
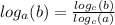
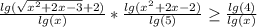
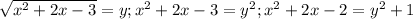

Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.
Пересечение множеств записывается так:
A ∩ B = {x | x ∈ A и x ∈ B}
На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.
Множества могут не пересекаться вообще, одно может полностью включать другое.
Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.
Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.
Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.
Объединение множеств описывается так:
A ∪ B = {x | x ∈ A или x ∈ B}
На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.
Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».
Сравните. Даны множества A = {1,2,3,4,5} и B = {4,5,8,9}. Разность множеств обозначается знаком \.
A \ B = {1,2,3}, т. к. 4 и 5 входят в множество B.
В то время как B \ A = {8,9}.
Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некого множества C до A.