1) «Человек произошёл от обезьяны» — популярный тезис, который обычно ассоциируют с дарвинистами.
Изображение с фронтисписа работы Хаксли Evidence as to Man’s Place in Nature (1863), на котором сопоставляются скелеты обезьян и человека.
Human evolution scheme.svg
Обычно идею приписывают Чарльзу Дарвину, однако она высказывалась и до него
2)Если говорить о виде homo sapiens, то есть «человеке разумном», он сравнительно молодой. Официальная наука дает ему около 200 тысяч лет. Такой вывод был сделан на основе исследования митрохондриальной ДНК и знаменитых черепов из Эфиопии. Последние были найдены в 1997 году во время раскопок вблизи эфиопской деревни Херто. Это были останки мужчины и ребенка, возраст которых насчитывал не менее 160 тысячи лет. На сегодняшний день это самые древние из известных нам представителей человека разумного. Ученые окрестили их homo Sapiens idaltu или «старейший разумный человек».
1. б) (-3; 8]
2. а)
3. x∈ [-1; 2)
4. x∈ (-3; +∞)
5. x∈ (-1,5; 6]
6. x∈ [1/5; 2]
7. x∈ (-∞; 12]
8. x∈ [-2; 3]
Пошаговое объяснение:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3.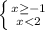
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4.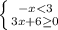
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:
1/5 ≤ x ≤ 2 или x∈ [1/5; 2]
7. Решите совокупность неравенств
Отсюда х ≤ 12 или x∈ (-∞; 12]
8.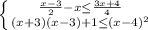
Отсюда -2 ≤ х ≤ 3 или x∈ [-2; 3]