90,270.-90 (если cosx=0)
или
45,225,-135 (если cosx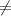 0)
0)
Пошаговое объяснение:
Произведение двух выражений равно 0, если
1) первое выражение равно нулю, т.е. cosx=0;
2) второе выражение равно нулю, т.е. sinx-cosx=0.
Решим отдельно первый и второй случаи.
1) cosx=0 => x=p/2+pk
2)sinx-cosx=0 => Поделим обе части выражения на cosx, который не равен нулю(если бы cosx=0, то делить нельзя, т.к. нельзя делить на ноль).
Получим sinx/cosx-cosx/cosx=0
Знаем, что sinx/cosx=tgx
Поэтому получим
tgx-1=0
Далее
tgx=1
x=p/4+pk
Получили ответ:p/2+pk или p/4+pk
Нам необходимо выбрать те углы, которые находятся в промежутке от -180 до 360.
p/2+pk = 90 + 180k (где k - целое число).
Подставляя вместо к различные целые числа, выберем те, которые удовлетворяют условию(от -180 до 360). Получим, что это углы
90,270 и -90
Аналогично со вторым ответом.
p/4+pk = 45 + 180k
Получим углы 45, 225,-135
Потому что константа не стоит одиноко, а составляет компанию двум иксам в кубе. Давайте по аналогии с производной для одной переменной. возьмем константу. ну ... например, ) 5.
5'=0
однако же..
(5x²)'=5*(x²)'=5*2х=10х, здесь не возникает вопросов, почему она не равна нулю? Отнеситесь к ней, как к обычному числу, т.е. дифференцируете по х, у константа, по у, х константа, т.е. число.
Во втором случае, по той же причине. 2x^3 - это константа, но рядом с ней у, константу выносим за знак производной, а производная у по у равна единице, умножили на константу, ее и получили.
Вот если бы Вы брали вторую частную производную по иксу во втором примере, тогда бы 6у обратился в нуль. т.к. производная чистой константы равна нулю.