Его характеристическое уравнение имеет вид:
k² + 4 = 0
k² = -4
Его корни k₁,₂ = 2i.
То есть в данном случае корни комплексные(k₁=α+βi,k₂=α-βi) и для них α = 0,β =2 Следовательно, решение однородного уравнения запишется в виде:
y(x) = C₁cos(βx) +C₂sin(βx) = C₁cos(2x) +C₂sin(2x)
Для нахождения функций C₁ и C₂ используем начальные условия:
y(0)=1; y'(0) = 2
y(0) =C₁cos(2*0) + C₂sin(2*0) = C₁ = 1.
Найдем производную функции:
y'(x) = -2C₁sin(2x) + 2C₂cos(2x).
Подставим начальное условие:
y'(0) = -2sin(0) + 2C₁cos(0) = 2С₁ = 2 ⇒С₁ = 1.
Следовательно частное решение дифференциального уравнения:
y(x) = cos(2x) + sin(2x)
Проверка: y'(x) = -2sin(2x) + 2cos(2x)
y''(x) = -4cos(2x) - 4sin(2x)
Подставляем в исходное уравнение
y'' + 4y = -4cos(2x) - 4sin(2x) + 4(cos(2x)+sin(2x)) = 0
ответ: y(x) = cos(2x) + sin(2x)
Найдем начала общее решение соответствующего однородного дифференциального уравнения
(*)
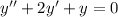Воспользовавшись заменой Эйлера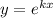 
, мы получим характеристическое уравнение
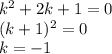
Общее решение уравнения (*)
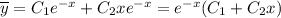
Далее нужно найти частное решение. Рассмотрим функцию:
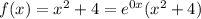
Здесь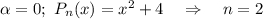 
Сравнивая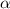 
с корнями характеристического уравнения и, принимая во внимая, что 
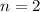частное решение будем искать в виде
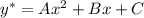
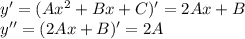
Подставляем все это в исходное дифференциальное уравнение
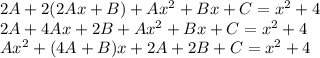
Приравниваем коэффициенты при степени x
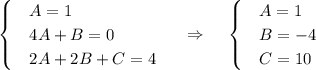
Частное решение: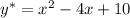 
Общее решение линейного неоднородного дифференциального уравнения:
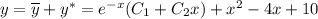
ответ:625