очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
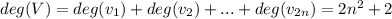
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
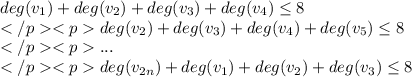
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.
Билгеле булганча, санның төп сүзлек фонды зур түгел. Татар лексикасында алынма миллион, миллиард һ.б. аннан да зуррак сүзләрне кертеп санамаганда, ул барлыгы 20 сүздән тора (берлек саннар, унлылар, йөз, мең сүзләре) (2; 76).
Сан төркемчәләре ягыннан күзәтсәк, "Хисаметдин менла" романында микъдар саны өстенлек алыр. Бу - табигый күренеш. Чөнки микъдар саны сан-исәп төшенчәсен, предметның билгесен белдергәндә кулланыла (2; 76). "Н" авылында 2 мәчет бар; Кәпик дәгел, 20 кәпик табармын, айда 6 монет, бәс елда 27 монет тапмамык мөхәльдер. Абстракт микъдар төшенчәсен белдергәндә микъдар саны мөстәкыйль кулланылган һәм грамматик категорияләргә ия була ала: 72 дән (чыгыш килеше) йөзгә (юнәлеш килеше) кадәр озак дәгел.
Тәртип саны микъдар саны нигезенә -нчы, -нче, -ынчы, -енче аффиксы кушып ясала (3; 105). Романда кулланылган тәртип саннары семантик яктан табигый санау тәртибендә предметларның эзлек-лелеген күрсәтү, һәм бу эзлеклелек предметларның төп билгесе булуы аңлашыла (2,79): икенче мәктәп, икенче бүлмә чигендә.