а) Можно. Для этого удобно брать палочки, идущие подряд. Возьмем первые 5 палочек: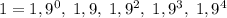 
.
Построим треугольник ABC: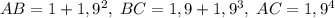 
. Заметим, что 
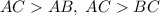, поэтому можно не рассматривать неравенства треугольника, включающие эту сторону. Осталось доказать, что 
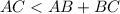. Действительно 
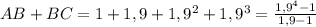по формуле суммы геометрической прогрессии. Но 
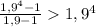. Проверим истинность этого неравенства: 
.
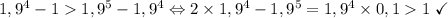б) Предположим, что можно. Тогда, в частности, можно составить два одинаковых отрезка. Рассмотрим набор степеней числа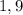 
, которые формируют первый отрезок. Пусть это числа 
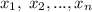, для второго отрезка возьмем степени 
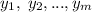. Получим 
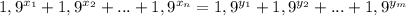(*). Теперь становится ясно, почему это не может быть верно. Ведь то, что мы видим, похоже на запись числа в системе счисления, пусть и "необычной". Но двух различных записей одного числа не бывает. Однако трудно говорить об этом, имея дробную систему счисления. Пусть 
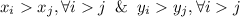, другими словами, степени расставлены по порядку. Умножим уравнение на 
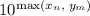, получим только целые числа вида 
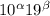. Пусть 
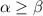. Выберем такое число 
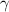, что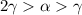 
. Тогда число 
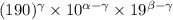записано в системе счисления 190, поскольку, как легко видеть, 
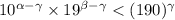. Отсюда и следует наше противоречие.
Впрочем, кажется, что это перебор, и можно было решить проще: в (*) вычеркнем равные члены с обеих сторон. Получим, что сумма разных степеней равна другой сумме разных степеней. Теперь в левой части к большим степеням перекинем с правой стороны меньшие, а для правой части наоборот. Значит, отрицательное число равно положительному. Противоречие.
Однако для тренировки, мне представляется, было полезно рассмотреть оба подхода.
С чего ты взял, что советник короля украл перец?
Если бы это был бы советник, то он бы не стал говорить, что "точно кто украл перец", он бы сказал "это был точно не я". А тут он возможно лжёт, но перец он не крал.
Хотя, возможно, что он скажет, что вор есть он сам, НО, тогда получается, что он НЕ СОВРЁТ, а скажет правду, а воры перцев всегда врут. Но, тут несостыковка. Он украл перец, но не соврал. Такого быть не может.
А возможно, что он скажет неправду, свалив вину на другого человека, тогда он действительно соврёт и может оказаться вором.
На эту задачу трудно дать верный ответ, можно лишь догадываться да или нет.
х=6-3,565
х=2,435