Пусть уравнения прямых имеют вид:
l₁:y=k₁x+m₁
l₂:y=k₂x+m₂
Прямые проходят через точку (5;25)
Подставим координаты точки в уравнения:
25=5k₁+m₁ ⇒m₁ =25-5k₁
25=5k₂+m₂ ⇒m₂=25-5k₂
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1):
k₁k₂=-1
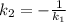
Пусть k₁=k, тогда 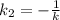
По условию: прямая l₁ пересекает ось Ox в точке (a;0)
Подставляем координаты точки в уравнение l₁:y=kx+ 25-5k
0=ka+25-5k
и пересекает график функции y=x² в точке (b;b²).
Подставляем координаты точки в уравнение l₁:y=kx+ 25-5k
b²=kb+25-5k
Прямая l₂ пересекает ось Ox в точке (c;0)
Подставляем координаты точки в уравнение l₂: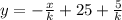
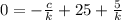
и пересекает график функции y=x² в точке (d;d²)
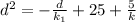
Получаем систему:
{0=ka+25-5k
{b²=kb+25-5k
{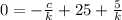
{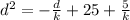
Перепишем:
{ka=5k-25
{kb=b²-25+5k
{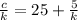
{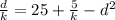
перемножаем:
abcd=
а) ||х - 12| - 2| = 5
|х - 12| - 2 = -5 или |х - 12| - 2 = 5
|х - 12| = -3 или |х - 12| = 7
нет корней, или х - 12 = -7, или х - 12 = 7
x = 5 или x = 19
ответ: 5; 19.
б) |||2х + 5| + 2| - 5| = 6
||2х + 5| + 2| - 5 = -6 или ||2х + 5| + 2| - 5 = 6
||2х + 5| + 2| = -1 -- ∅ или ||2х + 5| + 2| = 11
|2х + 5| + 2 = -11 или |2х + 5| + 2 = 11
|2х + 5| = -13 -- ∅ или |2х + 5| = 9
2х + 5 = -9 или 2х + 5 = 9
2x = -14 или 2х = 4
x = -7 или х = 2
ответ: -7; 2.
4кг×1=4кг