Пусть, для определённости, x<=y<=z (<= обозначает "меньше или равно"). Тогда хyz=x+y+z<=3z, т. е. хyz<=3z. Отсюда xy<=3, а поэтому х^2<=3. Так как x - натуральное, то x=1. Далее, если у=1, то из уравнения xyz=x+y+z следует, что z=2+z, что невозможно. Если y>=3, то из этого же уравнения следует, что 3z=z+4, т. е. z=2, а поэтому у>z, что невозможно. Таким образом, у<3, и следовательно, у=2. Подставляя значения х=1 и у=2 в уравнение xyz=x+y+z получим 2z=3+z, а отсюда z=3
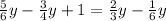
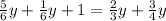
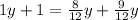
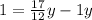
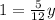


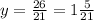
АВ=AМ/Sin(<ABM) = AM/Sin30 = AM/(1/2) = 2AM = 8.
По свойству ромба AD=AB=8.
Из прямоугольного треугольника АВМ <A=90-<ABM=90-30=60.
Из треугольника ABD по теореме косинусов
BD^2 = AB^2+AD^2-2*AB*AD*Cos(<A)=8^2+8^2-2*8*8*(1/2) = 64
BD=(64)^(1/2) = 8