Математика: Каким плохим качеством проявил себя ленин?

Каким плохим качеством проявил себя ленин?

👇

Ответ:

anuta136

24.04.2020

Здоровье подкачало, а так нормальный руководитель был, но не умел грамотно расчитывать что вытекет из определенных деяний

4,6(17 оценок)

Открыть все ответы

Ответ:

gribvlad123

24.04.2020

а) При значении а = -6 уравнение имеет корень равный 2.

При значении а = 16 уравнение имеет корень равный -3/4.

При значении а = 60 уравнение имеет корень равный -0,2.

b) При значении а = 0 уравнение не имеет корней.

c) При а > 0 уравнение будет иметь отрицательный корень.

Пошаговое объяснение:

Требуется найти, при каких значениях а уравнение

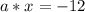$\displaystyle a*x=-12$ :

а)

1. Имеет корень, равный 2.

Подставим вместо х его значение 2 и решим уравнение относительно а:

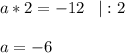
$\displaystyle a*2=-12\;\;\;|:2\\\\a=-6$

⇒ При значении а = -6 уравнение имеет корень равный 2.

2. Имеет корень, равный 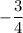$\displaystyle -\frac{3}{4}$ .

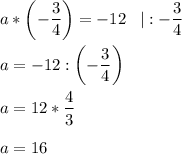
$\displaystyle a*\left(-\frac{3}{4} \right)=-12\;\;\;|:-\frac{3}{4} \\\\a=-12: \left(-\frac{3}{4}\right) \\\\a=12*\frac{4}{3}\\\\a=16$

⇒ При значении а = 16 уравнение имеет корень равный 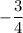$\displaystyle -\frac{3}{4}$ .

3. Имеет корень, равный -0,2.

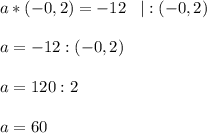
$\displaystyle a* (-0,2)=-12\;\;\;|:(-0,2)\\\\a=-12:(-0,2)\\\\a=120:2\\\\a=60$

⇒ При значении а = 60 уравнение имеет корень равный -0,2.

b) Не имеет корней.

Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.

Это возможно только тогда, когда а = 0.

Проверим:

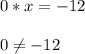
$\displaystyle 0*x=-12\\\\0\neq -12$

⇒ При значении а = 0 уравнение не имеет корней.

с) Имеет отрицательный корень.

Правая часть у нас отрицательная.

При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.

При делении чисел с разными знаками, частное - отрицательно.

⇒ а > 0

⇒ При а > 0 уравнение имеет отрицательный корень.

4,8(87 оценок)

Ответ:

hades77

24.04.2020

Пусть на второй полке было x книг, тогда на первой 3x книг. КОГДА с первой полки сняли 10 книг, то на ней осталось (3x-10)книг. Когда на вторую полку положили 30 книг, то на ней стало (x+30) книги. По условию задачи известно, что после этого на обеих полках книг стало поровну, т.е количество книг на первой полке (3x-10) = количеству книг на второй полке (x+30)

Составим уравнение:

3x-10=x+30

3x-x= 30+10

2x=40

X=40:2

X=20 книг на 2-ой полке

3х=20•3=60 книг на 1-ой полке

ответ:60 книг; 20 книг

Пошаговое объяснение:

4,5(1 оценок)

Это интересно:

Здоровье