 и
и 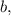 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
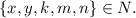
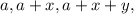 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и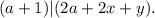
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;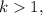 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.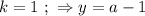 ;
;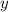 его значение
его значение 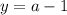 и будем искать такие комбинации
и будем искать такие комбинации 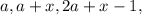 чтобы:
чтобы: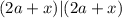 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 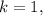
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и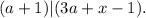
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;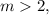 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.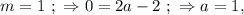 но это не подходит по условию.
но это не подходит по условию.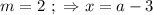 ;
; его значение
его значение 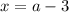 и будем искать такие комбинации
и будем искать такие комбинации 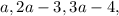 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 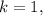
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 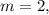
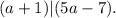
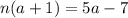 ;
;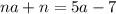 ;
; ;
;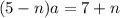 ;
;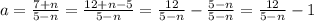 ;
;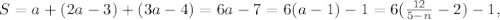
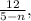 т.е. при
т.е. при 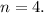
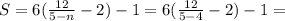
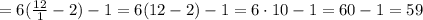 ;
;
Где он родился?
Сколько было у него братьев?
Где он познакомился со своей будущей женой?
Кем он был назначен после окончания двух курсов экономического института в Минске?
Чем он по жизни любил заниматься?
Где он учился после 7-летней школы?
Куда он поступил в 1931 году?
О чем Громыко не упомянул в своих мемуарах "Памятное"?
Кем стал Громыко в 1939 году?
Какую делегацию Громыко возглавлял в 1944 году?
В каком городе именем Андрея Громыко названы ушица и средняя школа №1?
В каком городе Громыко был установлен бронзовый бюст?
Сколько у Громыко орденов Ленина?
Как звали жену Громыко?
Чем увлекался Громыко?
Когда умер Андрей Громыко?
Где его похоронили?
Когда появились первые научные статьи Громыко?
Когда Громыко занимал должность председателя Президиума Верховного Совета СССР?
В каком году Громыко выступил против Молотова в поддержку Хрущева?
В каком году Громыко выступил против Хрущева в поддержку Брежнева?
С какого по какой год Громыко был членом ЦК КПСС?
Каких принципов по свидетельству и ученика Громыко, советского дипломата и доктора исторический наук, Андрей Громыко придерживался?
Какой договор был подписан при непосредственном участии Громыко 5 августа 1963 года?
Где у Громыко первая беседа с Павлом 6?
С кем Громыко чаще и охотнее, чем с кем либо, вёл переговоры?
Какие границы были заключены при деятельном участии Громыко?