1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
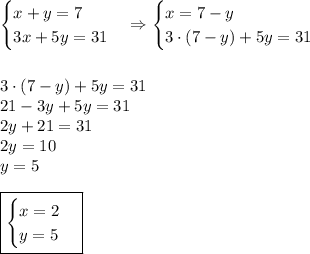 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
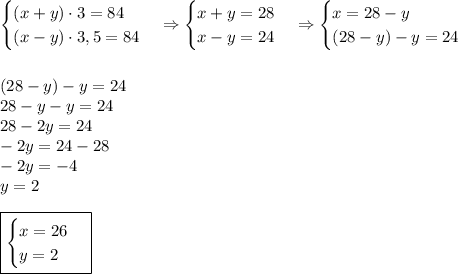
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
1
Пошаговое объяснение:
пусть в классе 30 учеников, тогда 60/30=2(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наибольшее число учеников без Маши
30+1=31 - это наибольшее число учеников с Машей
пусть в классе 10 учеников, тогда 60/10=6(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наименьшее число учеников без Маши
10+1=11 - это наименьшее число учеников с Машей
учеников не менее 10 и конфет не более 60 - решение соответствует условию задачи
1
Пошаговое объяснение:
пусть в классе 28 учеников, тогда 56/28=2(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наибольшее число учеников без Маши
28+1=29 - это наибольшее число учеников с Машей
пусть в классе 14 учеников, тогда 56/14=4(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наименьшее число учеников без Маши
14+1=15 - это наименьшее число учеников с Машей
учеников не менее 10 и конфет не более 60 - решение соответствует условию задачи
4+4+4=12 людей . 2+2+8=12 булок