Есть 2 варианта карт у Гали
а) 4, 6, 12
б) 4, 8, 10
Пошаговое объяснение:
1. Сумма всех чисел на всех 13 карточках равна
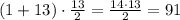
Суммы чисел - одинаковы у 4х человек,
у каждого из 4рых по 3 карточки.
Пусть, потеряна карточка с числом х.
Очевидно, что оставшиеся 12 карточек в сумме дают число в промежутке
78 ≤ 91-х ≤ 90
Также очевидно, что
91 - х = 4а
Из промежутка [78; 90] кратны 4 только числа:
80; 84; 88
80 - исключаем, т.к. тогда потеряна карта 11, а она у Ани
84 - исключаем, т.к тогда теряется карта 7, а она у Толика
Значит, сумма чисел на руках у 4х человек = 88
И потеряна карта 3
А на руках 6 - четные и 6 нечетные карточки
А это - 4 тройки карт;
И сумма для каждой тройки равна 88/4 = 22
Ане досталась карточка 11
и еще пара карт с суммой 11
Толику 7
и еще пара карт с суммой 15
Гене 9
и еще пара карт с суммой 13
Заметим: суммы у каждой из "ещё пары карт" нечетные. А это значит, что одно число из этой пары нечетное.
Вместе с тремя известными нечетными картами получается, что все 6 нечетных карточек на руках у Ани, Толи т Гены.
У Гали же все 3 карты четные
Карточка 13 может быть только одной из пары у Толика (Гена в пролете, так как у него 13 в паре, а карточки 0 нет). И ещё 2 до нужной суммы
Итого:
Потеряна: 3
ТОЛЯ: 7, 13, 2
АНЯ: 11, ?, ?
ГЕНА: 9, ?, ?
Из нечетных не распределили: 1 и 5 Их можно распределить
1 Ане и 5 Гене
5 Ане и 1 Гене
Так мы просчитали полные наборы у троих ребят из четверых
Значит Гале достаются 3 "непосчитанные" карты:
1) (Потеряна: 3)
ТОЛЯ: 7, 13, 2
АНЯ: 11, 1, 10
ГЕНА: 9, 5, 8
ГАЛЯ: 4, 6, 12
------------------
2) (Потеряна: 3)
ТОЛЯ: 7, 13, 2
АНЯ: 11, 5, 6
ГЕНА: 9, 1, 12
ГАЛЯ: 4, 8, 10
Приступим к уроку мат. анализа
1)
a) Для поиска вертикальных асимптот нужно рассмотреть односторонние пределы в окрестностях несуществования функции
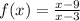
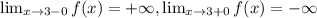
x=3 - вертикальная асимптота
![]\lim_{x \to 9-0} f(x)=-\infty, \lim_{x \to 9+0} f(x)=+\infty](/tpl/images/0065/8887/ae326.png)
x=9 - вертикальная асимптота
ответ: 12
б) 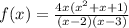
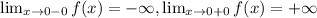
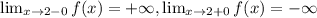
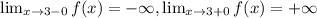
x=0, x=2, x=3 - вертикальные асимптоты
ответ: 5
________________________________________________________________________
2) ![\sqrt[9]{x+1}=1+\frac{1}{9}x+\frac{\frac{1}{9}(\frac{1}{9}-1)}{2}x^2](/tpl/images/0065/8887/3da6b.png)
![\sqrt[9]{1+0,4}=1+1/9-(4/81)*0,4^2=2099/2025\approx1,037](/tpl/images/0065/8887/c7b02.png)
________________________________________________________________________
3)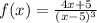
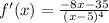
x=-35/8
При переходе через эту точку производная меняет свой знак c + на -, т.е. это точка локального максимума
ответ: -4,375
________________________________________________________________________
4)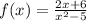
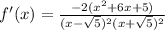
критические точки = x=-√5, x=√5, x=-1, x=-5
производная меняет свой знак с - на + в точке x=-5 - точка лок. минимума
ответ: -5
________________________________________________________________________
5)
а) Найдем точки пересечения
6x-4=x²+5x-6
x²-x-2=0
x₁=-1 x₂=2
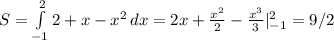
б) Точки пересечения
-x+7=x²-x+3
x²-4=0
x₁=-2, x₂=2
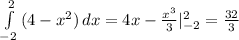
________________________________________________________________________
6)
a) 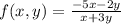

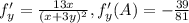
направляющий вектор {1/√10, 3/√10}
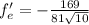
б) 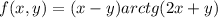
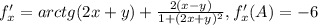
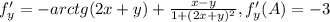
направляющий вектор {-2/√29, -5/√29}
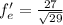
_______________________________________________________________________
7) 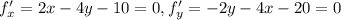
x=-3, y=-4 - стационарная точка
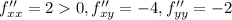
![\left[\begin{array}{cc}2&-4\\-4&-2\end{array}\right]=-20<0](/tpl/images/0065/8887/c91d0.png)
экстремумов нет
Прямой угол - то угол, градусная мера которого равна 90°.
Тупой угол - это угол, градусная мера которого больше 90°.
Острый угол - это угол, градусная мера которого меньше 90°.
На рисунке 1 синим цветом отмечены острые углы, красным цветом отмечены тупые углы. Угол под номером 3 не отмечен, так как он прямой.
На рисунке 2:
∠AOB = 90°, прямой угол.
∠CDE = 60°, острый угол, его градусная мера < 90°.
∠MKN = 120°, тупой угол, его градусная мера > 90°.
(Для сравнения, прямой угол отмечен зеленым пунктиром).