Пусть х км/ч - скорость на обратном пути, тогда (х + 3) км/ч - от дома до станции; 30 мин = 0,5 ч. Уравнение:
30/х - 30/(х+3) = 0,5
30 · (х + 3) - 30х = 0,5 · х · (х + 3)
30х + 90 - 30х = 0,5х² + 1,5х
90 = 0,5х² + 1,5х
0,5х² + 1,5х - 90 = 0
Разделим обе части уравнения на 0,5
х² + 3х - 180 = 0
D = b² - 4ac = 3² - 4 · 1 · (-180) = 9 + 720 = 729
√D = √ 729 = 27
х₁ = (-3-27)/(2·1) = (-30)/2 = -15 (не подходит, т.к. < 0)
х₂ = (-3+27)/(2·1) = 24/2 = 12 (км/ч) - скорость на обратном пути
(х + 3) = 12 + 3 = 15 (км/ч) - скорость от дома до станции.
ответ: 15 км/ч.
-15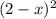
Пошаговое объяснение:
Самый простой — через уравнение и теорему Виета
-60 + 60x - 15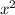
= 0
D =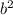 
- 4ac = 
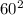- 4·(-15)·(-60) = 3600 - 3600 = 0
Т. к. дискриминант равен 0, квадратное уравнение имеет один действительный корень:
x =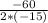 
= 2
По теореме Виета -60 + 60x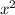 - 15 = -15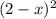
Но у меня подозрение, что это вы ещё не проходили, так что считайте всё вышесказанное проверкой правильности этого решения:
Вынесем -15:
-15(4 - 4x + )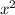
Сгруппируем
-15((4 - 2x)(-2x + ))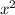
Выносим за скобки 4 и x соответственно:
-15(2(2 - x) - x(2 - x)) <=> -15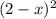
63:(х-6):8=80-24
63:(х-6):8=56
63:(х-6)=56:8
63:(х-6)=7
х-6=63:7
х-6=9
х=9+6
х=15