Это показательное уравнение вида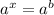 
, где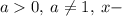 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения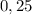 
представить в виде числа со степенью так, чтобы в основании было число 
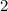. Это явно число 
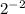(проверка: 
).
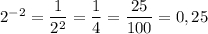Значит теперь, когда наше показательное уравнение имеет вид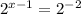 
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение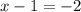 
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
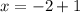Из этого следует, что ответ нашего показательного уравнения равен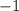 
.
1)Пусть в гору ехал х часов, под гору ехал у часов. Тогда получим систему:
{60х=120у, х+у=4
х=4-у
Подставим в первое уравнение:
60(4-у)=120у
240-60у=120у
240=180у
у= 4/3 (часов)
х=4-(4/3)=2 2/3 (часов)
60* (2 2/3)=160км - расстояние между пунктами
(160+160)/4=320/4=80км/ч - средняя скорость автомобиля
ответ. 160 км и 80 км/ч
2)270*0.05=13.5гр золота в сплаве
Пусть надо добавить х гр золота. Тогда масса нового сплава равна 270+х гр, масса содержащегося в нем золота 13,5+х гр. и эта масса равна 0,1 массы всего сплава:
13,5+х=0,1(270+х)
13,5+х=27+0,1х
0,9х= 13,5
х=15 гр - золота нужно добавить.
ответ. 15 гр золота.
а синих=(12+х). Т.к. всего шаров 93, составим уравнение:
х+(х-12)+(12+х)=93
3х=93, х=31 шт - кол-во белых шаров
Отсюда следует кол-во красных = 31-12=19 шт, а синих=12+31=43 шт.