Если в цилиндре осевое сечение - квадрат, то радиус основания в два раза меньше образующей. Образующая цилиндра равна высоте.
Как и сказала, радиус основания = 1/2 * 14 см = 7 см.
А объём цилиндра равен произведению площади основания на высоту.
То есть :
V(цилиндра) = (7 см)²*14 см*π = 686 см³*π.
ответ : 686 см³*π.Задача №3.Брусок имеет форму прямоугольного параллелепипеда.
Находим объём чугунного бруска. Он равен произведению трёх его измерений :
V(чугунного бруска) = 5,5 см*20 см*40 см = 4400 см³.
А массу найдём по этой формуле :
m = p*V
Где m - масса тела, p - плотность вещества, из которого изготовлено тело, V - объём тела.
Подставляем и считаем :
m = (7,5 г/см³) * 4400 см³ = 33000 г = 33 кг.
ответ : 33 кг.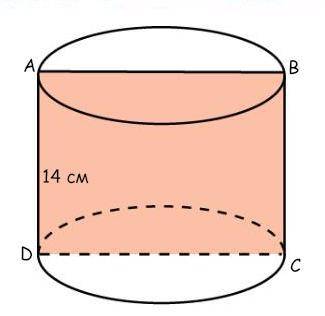
1. Пусть это число такое 10a + b, где b - последняя цифра числа, а - все остальные цифры, т.е. некое число.
10a + b - 2018 = a
9a = 2018 - b
Чтобы число делилось на 9, сумма его цифр должна делиться на 9. Значит, b=2. Тогда, 9a = 2018 - 2 = 2016; a = 224.
Итак, искомое число 2242.
Проверяем, 2242 - 224 = 2018
2. Составим 2 трёхзначных числа:
100a+10b+c и 100d+10e+f
Найдём разницу:
100a+10b+c-100d-10e-f = 100(a-b) + 10(b-e) + (c-f) = 693
Откуда,
a-d = 6
b-e = 9
c-f = 3
Если взять наибольшее трёхзначное число 999, то наименьшее возможное равно 999 - 693 = 306. Т.к. нуль не м.б. ни в каком числе, то ближайшее наименьшее возможное число равно 299, тогда наибольшее возможное равно 299 + 693 = 992
3. Пусть первая цифра равна а, а вторая равна b, тогда третья цифра равна (a+b), четвёртая - (a+2b), пятая - (2a+3b), шестая - (3a+5b).
При этом, (3a + 5b) д.б. меньше 10, т.к. это цифра. При b>1 неравенство 3a+5b<10 не выполняется. При b=1 неравенство превращается такое 3a<5 и a=1. При b=0 неравенство будет такое 3а<10, и а=3. Т.к. число ищем максимальное, то берём а=3. Значит, максимальное искомое число равно: 303369
ответ: 303369
Подберём
т.е. из первой 34 из второй 45